- #1
PainterGuy
- 940
- 69
Hi,
The following is my basic understanding of blackbody radiation spectrum. The important sections are in boldface.
Question 1:
The quote above says that at room temperature (let's say 20 C or 293 K) the emission is in the infrared region. You can see in the figure below, lower curve, that at temperature of 37 C (little higher than room temperature), the curve extends well into longer wavelengths such as microwave and beyond. Is it really true that a blackbody at 37 C radiates microwaves and radio waves etc. as shown in the figure below? I don't think so. Then, why is the curve shown this way?
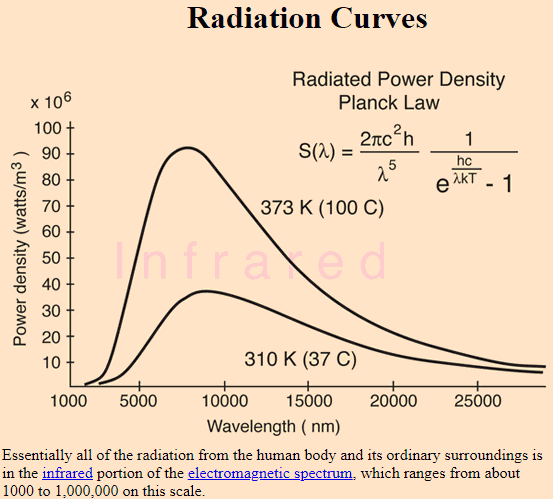
Source: http://hyperphysics.phy-astr.gsu.edu/hbase/bbrc.html
My own attempt at answer using the Wikipedia article, en.wikipedia.org/wiki/Black-body_radiation :
Real objects never behave as full-ideal black bodies, and instead the emitted radiation at a given frequency is a fraction of what the ideal emission would be.
A black body radiates energy at all frequencies, but its intensity rapidly tends to zero at high frequencies (short wavelengths). For example, a black body at room temperature (300 K) with one square meter of surface area will emit a photon in the visible range (390–750 nm) at an average rate of one photon every 41 seconds, meaning that, for most practical purposes, such a black body does not emit in the visible range.Question 2:
Most of the time I haven't seen that the size of blackbody is mentioned. For example, if sun is approximated as a blackbody, its temperature is almost 5800 K. There could be another blackbody of tennis ball size which is also at temperature of 5800 K. I don't think that power radiated by them is the same. The tennis ball size blackbody will radiate less power. The figure below uses spectral radiance units, kW/(sr.m^2.nm), but the figure above, used for Question 1, uses power density units, watts/m^3.
Which unit is more descriptive? Why size is not mentioned? Perhaps, the unit conveys this information indirectly.
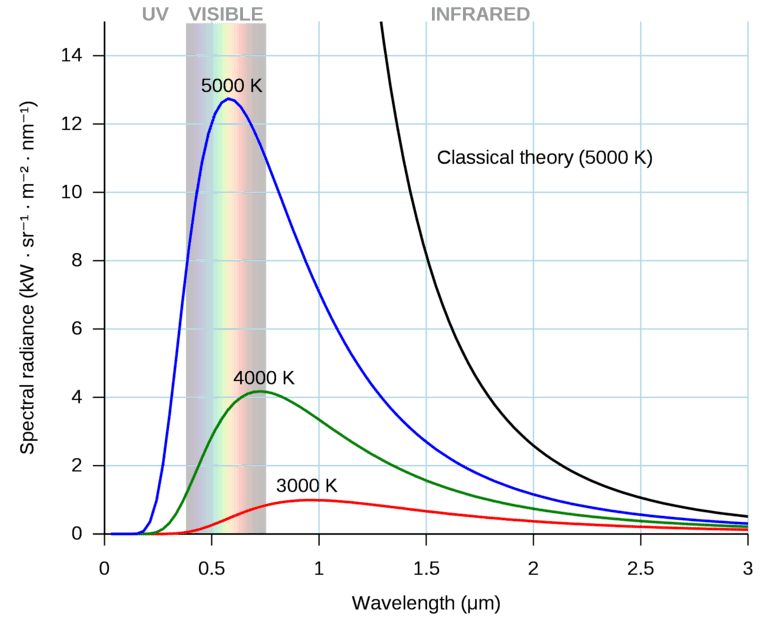
Source: en.wikipedia.org/wiki/Black-body_radiationQuestion 3:
The Wikipedia article, en.wikipedia.org/wiki/Black-body_radiation, says that an almost perfect black-body spectrum is exhibited by the cosmic microwave background radiation. It's related to Question 1.
Was CMB always more like a blackbody radiation, or it started acting more like radiation from a blackbody as the time passed and universe expanded?
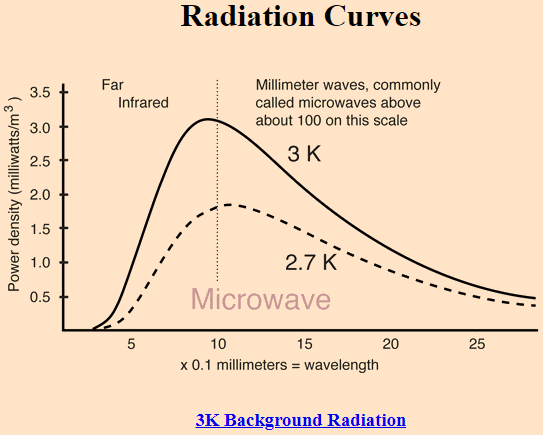
Source: http://hyperphysics.phy-astr.gsu.edu/hbase/bbrc.html
Thank you for your help and time!
Helpful links:
1: https://physics.stackexchange.com/questions/225207/is-sun-a-black-body
2: https://physics.stackexchange.com/q...-be-that-the-sun-emits-more-than-a-black-body
3: https://en.wikipedia.org/wiki/Radiance
4: https://chem.libretexts.org/Bookshelves/Physical_and_Theoretical_Chemistry_Textbook_Maps/Physical_Chemistry_(LibreTexts)/01:_The_Dawn_of_the_Quantum_Theory/1.01:_Blackbody_Radiation_Cannot_Be_Explained_Classically
The following is my basic understanding of blackbody radiation spectrum. The important sections are in boldface.
Source: https://en.wikipedia.org/wiki/Black-body_radiation#SpectrumBlack-body radiation has a characteristic, continuous frequency spectrum that depends only on the body's temperature, called the Planck spectrum or Planck's law. The spectrum is peaked at a characteristic frequency that shifts to higher frequencies with increasing temperature, and at room temperature most of the emission is in the infrared region of the electromagnetic spectrum.
...
A black body at room temperature radiates only in the infrared spectrum and cannot be perceived by the human eye, [6] but some reptiles can sense... As the object becomes a little hotter (about 500°C, 900°F or 800K), the emission spectrum gets stronger and extends into the human visual range, and the object appears dull red. As its temperature increases further, it emits more and more orange, yellow, green, and blue light (and ultimately beyond violet, ultraviolet).
Question 1:
The quote above says that at room temperature (let's say 20 C or 293 K) the emission is in the infrared region. You can see in the figure below, lower curve, that at temperature of 37 C (little higher than room temperature), the curve extends well into longer wavelengths such as microwave and beyond. Is it really true that a blackbody at 37 C radiates microwaves and radio waves etc. as shown in the figure below? I don't think so. Then, why is the curve shown this way?
Source: http://hyperphysics.phy-astr.gsu.edu/hbase/bbrc.html
My own attempt at answer using the Wikipedia article, en.wikipedia.org/wiki/Black-body_radiation :
Real objects never behave as full-ideal black bodies, and instead the emitted radiation at a given frequency is a fraction of what the ideal emission would be.
A black body radiates energy at all frequencies, but its intensity rapidly tends to zero at high frequencies (short wavelengths). For example, a black body at room temperature (300 K) with one square meter of surface area will emit a photon in the visible range (390–750 nm) at an average rate of one photon every 41 seconds, meaning that, for most practical purposes, such a black body does not emit in the visible range.Question 2:
Most of the time I haven't seen that the size of blackbody is mentioned. For example, if sun is approximated as a blackbody, its temperature is almost 5800 K. There could be another blackbody of tennis ball size which is also at temperature of 5800 K. I don't think that power radiated by them is the same. The tennis ball size blackbody will radiate less power. The figure below uses spectral radiance units, kW/(sr.m^2.nm), but the figure above, used for Question 1, uses power density units, watts/m^3.
Which unit is more descriptive? Why size is not mentioned? Perhaps, the unit conveys this information indirectly.
Source: en.wikipedia.org/wiki/Black-body_radiationQuestion 3:
The Wikipedia article, en.wikipedia.org/wiki/Black-body_radiation, says that an almost perfect black-body spectrum is exhibited by the cosmic microwave background radiation. It's related to Question 1.
Was CMB always more like a blackbody radiation, or it started acting more like radiation from a blackbody as the time passed and universe expanded?
Source: http://hyperphysics.phy-astr.gsu.edu/hbase/bbrc.html
Thank you for your help and time!
Helpful links:
1: https://physics.stackexchange.com/questions/225207/is-sun-a-black-body
2: https://physics.stackexchange.com/q...-be-that-the-sun-emits-more-than-a-black-body
3: https://en.wikipedia.org/wiki/Radiance
4: https://chem.libretexts.org/Bookshelves/Physical_and_Theoretical_Chemistry_Textbook_Maps/Physical_Chemistry_(LibreTexts)/01:_The_Dawn_of_the_Quantum_Theory/1.01:_Blackbody_Radiation_Cannot_Be_Explained_Classically