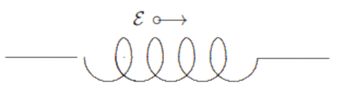hidemi
- 206
- 36
- Homework Statement
- The diagram (see attachment) shows an inductor that is part of a circuit. The direction of the emf induced in the inductor is indicated. Which of the following is possible?
A. The current is constant and rightward
B. The current is constant and leftward
C. The current is increasing and rightward
D. The current is increasing and leftward
E. None of the above
The answer is D.
- Relevant Equations
- ε = -L* dI/dt
I understand that the current is going rightward because of the negative sign in the equation above, but why is the current increasing not decreasing?
The current doesn't stay constant because it changes with the time based upon the equation above again.
The current doesn't stay constant because it changes with the time based upon the equation above again.