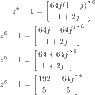The distinct roots of complex number
- Thread starter timeforchg
- Start date
-
- Tags
- Complex Complex number Roots
Click For Summary
Homework Help Overview
The discussion revolves around finding the distinct roots of a complex number equation, specifically focusing on the equation involving \( z^6 - 1 \) and a complex constant. Participants explore various methods to approach the problem, including polynomial expansion and polar form representation.
Discussion Character
- Mixed
Approaches and Questions Raised
- Some participants suggest expressing complex numbers in polar form to simplify calculations. Others discuss the potential of multiplying out the polynomial to find roots. Questions arise about the derivation of certain equations and the handling of complex numbers in different forms.
Discussion Status
Participants are actively engaging with the problem, sharing their thoughts and methods. Some have offered guidance on how to express complex numbers and suggested strategies for equating real and imaginary parts. There is no explicit consensus, but multiple lines of reasoning are being explored.
Contextual Notes
One participant notes that the problem is based on a past exam question, indicating a lack of provided solutions for verification. This context may influence the approaches taken and the urgency of finding a resolution.
Similar threads
- · Replies 21 ·
- · Replies 20 ·
- · Replies 19 ·
- · Replies 14 ·
- · Replies 18 ·
- · Replies 0 ·
- · Replies 3 ·
- · Replies 17 ·