The limit of the perimeter of a Koch snowflake as s(0) goes to zero

[nomadreid]

TL;DR

Letting the original triangle of the iteration that results in the Koch snowflake =s: Taking the limit of the Koch snowflake perimeter as s goes to zero intuitively would be infinity, although at s=0 the perimeter would be zero. I'm not sure how that works as an iterated limit.

On one side, if I have any finite value of s = the side of the original triangle of the Koch snowflake iteration, then the perimeter is infinite, so intuitively

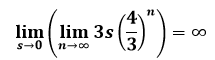
On the other hand, if I looked at the end result first and considered how it got there, then intuitively

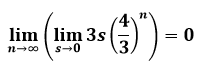
(Obviously at n=infinity and s=0, the perimeter is zero, but I am wondering about the limits)

These are the intuitive answers, but intuition is a lousy guide, so I am not sure how this works out as an iterated limit.
Thanks for any pointers.

(Note: this is not a homework question or part of any course, so if the problem is not well posed, I am the clumsy one.)

 

[fresh_42]

$\lim_{n \to \infty} \left(3s\cdot \left(\dfrac{4}{3}\right)^n\right)=\infty$ and $\lim_{s \to 0} \left(3s\cdot \left(\dfrac{4}{3}\right)^n\right)=0.$ Now, do whatever is allowed to $\infty$ and $0$, e.g. writing $\lim_{T \to C}$ in front of it.What do you really want to know?

 

[nomadreid]

$\lim_{n \to \infty} \left(3s\cdot \left(\dfrac{4}{3}\right)^n\right)=\infty$ and $\lim_{s \to 0} \left(3s\cdot \left(\dfrac{4}{3}\right)^n\right)=0.$ Now, do whatever is allowed to $\infty$ and $0$, e.g. writing $\lim_{T \to C}$ in front of it.What do you really want to know?

First, I am not sure whether your "T" and "C" are just repeating what I wrote, being n, s, 0, infinity... and what you mean by "whatever is allowed". What I would like to know is what would be the area of the Koch snowflake as s tends to zero--- infinity (my guess) or zero. Which order of the limits is the correct way to look at it?

 

[fresh_42]

The limits are what you have written. They are real numbers, resp. infinite big. Putting another limit in front of it doesn't change that. Limits are no procedures. If you want to establish a procedure, then we need to know what $n\longmapsto s(n)$ or likewise $s\longmapsto n(s)$ is.

 

[nomadreid]

The limits are what you have written. They are real numbers, resp. infinite big. Putting another limit in front of it doesn't change that. Limits are no procedures. If you want to establish a procedure, then we need to know what $n\longmapsto s(n)$ or likewise $s\longmapsto n(s)$ is.

Thanks. If I understand what you are getting at, the answer will depend on whether I treat s and n as independent variables, which order I wish to approach the limit, and if they are dependent variables, what the relationship between s and n would be. This makes sense. Thanks again.

 

[mathman]

My gut feeling $$\infty$$ is the correct limit. It reminded me of a problem I worked on with an approximate delta function near zero, where the sequence to zero at every point, but the integral remained positive.

 

[fresh_42]

My gut feeling $$\infty$$ is the correct limit. It reminded me of a problem I worked on with an approximate delta function near zero, where the sequence to zero at every point, but the integral remained positive.

Only in the case $s>0$. No sidelength, no perimeter. It is important to avoid any impression of a limit as a procedure. This is wrong. A limit is a unique, single element of $\mathbb{R}\cup \{\pm\infty \}.$

 

[WWGD]

Maybe, at least to get a feel, you can use the Log Limit? Or try for specific values of s that may be easy to compute/intuit, like $s=1/n$ Edit: I think @mathman may be right. Reminds me of the whole( paraphrase) " Coastline of Britain has infinite length) topic, where when you make your resolution/yardstick increasingly smaller, the perimeter goes to $\infty$.

 

[Filip Larsen]

Since the Koch curve is a fractal it may give a good context to also look at how limits are used for calculating fractal dimension rather than "just" settling with integer dimension limits that goes towards infinity or zero.

 

[pbuk]

There is some confusion here: $s$ is the initial side length when $n = 0$, it does not vary with $n$. So we don't need to consider $\lim_{s \to 0}$, we can just plug $s = 0$ into the equation and every term becomes 0.

Alternatively, use the iterative equation for the perimeter $P_{n+1} = \frac 4 3 P_n$. You can see that if $s = 0, P_0 = 3 s = 0$ and every iteration has zero perimeter.

 

[nomadreid]

So we don't need to consider lim_s→0, we can just plug s=0 into the equation and every term becomes 0.

The question was about the limit as one varied the initial side length; that is,
s=1 ⇒limit_n→∞perimeter of snowflake =∞
s=1/2 ⇒limit_n→∞perimeter of snowflake =∞
s=1/4 ⇒limit_n→∞perimeter of snowflake =∞
...
s>0 ⇒limit_n→∞perimeter of snowflake =∞

At s=0, of course, the perimeter =0, but no one assumes continuity, so the limit and the value attained need not be the same value.