The Q factor of the nuclear reaction problem?

[patric44]

Homework Statement

i have a problem deriving the following equation involving the Q factor and the energies of the residual nucleus and the outgoing particle in a nuclear reaction ?

Relevant Equations

the equation is attached

after using the conservation of energy and momentum for a nuclear interaction i arrived to the following equation for the q factor as the book did
, but can't get my head around deriving the second equation from the Q equation ?

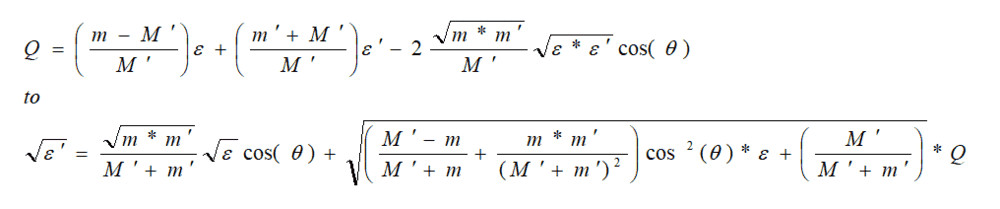
i will appreciate any help .
thanks

 

[kuruman]

Have you tried the substitution $\sqrt{\epsilon '}=x$? That should give you a quadratic equation in $x$. I have not done it, but that's what I would try first.

Edit: It looks like $Q$ must be under the radical to make the units come out right.

 

[patric44]

Have you tried the substitution $\sqrt{\epsilon '}=x$? That should give you a quadratic equation in $x$. I have not done it, but that's what I would try first.

Edit: It looks like $Q$ must be under the radical to make the units come out right.

thanks a lot it worked