- #1
Coffee_
- 259
- 2
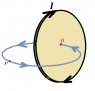
Background: Using Biot-Savart law we proved that for a closed loop with current ##I##, the magnetic field at a point P was equal to ##\vec{B}=-\frac{\mu_{0} I \nabla{\Omega}}{4 \pi}## where ##\Omega(x,y,z)## is a function of the position of P that represents the solid angle at which the loop is seen from P. The convention for the sign of ##\Omega## is that using the right hand rule to define the normal vector ##\vec{n}##, the solid angle is positive at the side towards which ##\vec{n}## points.
Problem: When trying to derive the circulation/closed loop integral of ##\vec{B}## using this information it's easy to see that it's 0 for any closed path that does not pass through this loop which agrees with Maxwell. However when going through the loop, I get a wrong sign. Let's take the situation where the integration path taken penetrates the loop from the negative side of the solid angle towards the positive. The only contribution for the passing through is from the penetration of the loop. ##\nabla \Omega . \vec{ds}=d\Omega=4\pi## in this case. Using this reasoning I get Circulation(##\vec{B}##)=##-\mu_{0}I## instead of a plus sign. Where have I messed up?
Problem: When trying to derive the circulation/closed loop integral of ##\vec{B}## using this information it's easy to see that it's 0 for any closed path that does not pass through this loop which agrees with Maxwell. However when going through the loop, I get a wrong sign. Let's take the situation where the integration path taken penetrates the loop from the negative side of the solid angle towards the positive. The only contribution for the passing through is from the penetration of the loop. ##\nabla \Omega . \vec{ds}=d\Omega=4\pi## in this case. Using this reasoning I get Circulation(##\vec{B}##)=##-\mu_{0}I## instead of a plus sign. Where have I messed up?