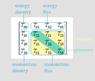
The diagonal components T_11, T_22, T_33 describe the flux of momentum (pressure).
The spatial components of the 4-momentum vector (T_01, T_10, etc.) describe the flux of energy (momentum).
I think that it is natural to reason that one does not require relative motion in order for pressure to occur, or viscosity for that matter (which covers the remaining stress-energy tensor components). I suppose that you could think of the 4-momentum vector as describing the motion of all particles in a unified direction (or lack thereof), where pressure describes the individual particle behaviour (which is taken to be random in direction). Literally, even though a (portion of a) cloud of gas may be at rest with respect to you, its individual particles still carry their own momentum along with them (this is pressure, particles pushing against you). However, when you switch your frame of reference to include only a single atom of gas, then the context immediately changes from pressure (momentum flux) back to momentum (energy flux), since the motion once again becomes unified in direction (it's impossible for the direction NOT to be unified when there's only one particle under consideration).
Things get a little strange when you consider viscosity to be the flux of pressure, or that viscosity is the diffusion of momentum (this springs a little more naturally from the Navier-Stokes equations).
Schutz's book "A first course in general relativity" has a great chapter on this, and always seems to do a better job at explaining it than I can.