- #1
timmdeeg
Gold Member
- 1,456
- 278
How do the components of the stress-energy tensor act on gravity regarding
a) the FRW-universe?
b) a solid ball?
In a FRW-universe ##\rho + 3P## determines the second derivative of the scale factor. So, there are no non-diagonal components. Just theoretically, if the perfect fluid was elastic, how would this show up in the SET?
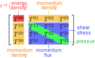
Now to the solid ball. How does pressure, shear stress and momentum flux influence the spatial curvature?
Does it make sense to say that these components increase or decrease the effective mass of the ball depending on their sign?
I'm not sure if shear stress and momentum flux can be positiv and negative as well. It would be great to have some examples how to achieve that.
Thanks.