Thermodynamics p-v cycle problem

[WrongMan]

Homework Statement

a system uses monoatomic ideal gas describing the following cycle (quasi static)
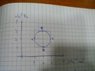
and basically the p-v graph is a circle,and it starts on the left side of the circle with states A, B, C, D (so that B and D are top an bottom) and so P on A (P_A) is equal to P_C and V_B= V_D
given values:
Cv=3/2R
P_A=P_C= 2*10⁵Pa
P_D=1*10⁵Pa
P_B=3*10⁵Pa
V_A=0.001m³
V_B=V_D=0.002m³
V_C=0.003m³.
what is the work done by the gas?

The Attempt at a Solution

so iv realized B to C and D to A are isothermal and i can calculate work for those, but the other two arent and they also arent adiabatic.
Im lost. there are so many relations due the first law, i don't know what to do. please a hint.

 

[TSny]

Even though states B and C are at the same temperature, the circular arc that connects them on the PV diagram is not an isothermal process.

Have you covered the relation between the "area under the curve" of a process on a PV diagram and the work done by the system during the process?

 

[WrongMan]

yes remember reading something like its the area enclosed by the cycle, but we haven't used that in exercises yet i guess.
and this isn't really a circle i think it would resemble something more like 4 triangles since there is 10⁸ orders of magnitude diference, no?

 

[TSny]

It will be a circular shape if the axes are scaled appropriately. But, as you say, if you then change the scale of one of the axes, the process would be elliptical rather than circular.

Yes, the work done by a cycle on a PV diagram is represented by the area (measured in Joules) enclosed by the cycle. Suppose you draw a square around the circle such that the circle is inscribed in the square. For the square cycle, how much work (in Joules) would be done by the gas if you go clockwise around the square?

 

[WrongMan]

0.001*10⁵. so is it that simple?

 

[TSny]

0.001*10⁵. so is it that simple?

How did you get this answer for the area of the square? How tall is the square (in units of Pa)? How wide is the square (in units of m³)?

 

[WrongMan]

How did you get this answer for the area of the square? How tall is the square (in units of Pa)? How wide is the square (in units of m³)?

im sorry, it's late over here, that's one fourth of the intended square.
its 0.002 m³ * 2*10⁵ Pa

 

[TSny]

im sorry, it's late over here, that's one fourth of the intended square.
its 0.002 m³ * 2*10⁵ Pa

Yes. Simplify that (including the units).

Use this answer to get the area of the circle.

 

[WrongMan]

ok so I've got further questions for this. (pic of cycle added)
1. what is the internal energy difference bettween points A and C
2. what is the liquid heat that passes through the system through paths (a))ABC and (b))AC ( this was exam question i don't fully remember the words used + translation problems)

So 1 seems straight forward for monoatomic ideal gases U depends only on T (U=3/2nRT) i find T for A and C using the state eq. for gases since i have p,v and n.(let R1 be result of this question)

for 2 starting with path AC so b): dQ-Pdv=R1. ----- Pdv= 2*10⁵*2*10^-3 and so dQ=dU+pdv
a) since Tc and Tb are equal then dU=0 and so all the U change lies in the path A-B... this i where i get confused... how do i find work for varying temperature, pressure and volume? is this adiabtic an dQ=0?
And for path BC dt=0 so dQ=pdv and again same question work for varying pressure and volume? (do i stil use p=nRT/V and integrate from vb to vc since T is constant here?) ok i just found that this part in parenthisis is correct - so my doubt is path A-B

 

[TSny]

2. what is the liquid heat that passes through the system through paths (a))ABC and (b))AC ( this was exam question i don't fully remember the words used + translation problems)

I'm not sure what "liquid heat" refers to. For part (b), I'm not sure what the path AC means. I guess it means the horizontal path from A to C. Not sure.

So 1 seems straight forward for monoatomic ideal gases U depends only on T (U=3/2nRT) i find T for A and C using the state eq. for gases since i have p,v and n.(let R1 be result of this question

OK

for 2 starting with path AC so b): dQ-Pdv=R1. ----- Pdv= 2*10⁵*2*10^-3 and so dQ=dU+pdv

You are not dealing with infinitesimal changes here. So, you should write ΔQ - ∫Pdv = ΔU.

a) since Tc and Tb are equal then dU=0 and so all the U change lies in the path A-B... this i where i get confused... how do i find work for varying temperature, pressure and volume? is this adiabtic an dQ=0?
And for path BC dt=0 so dQ=pdv and again same question work for varying pressure and volume? (do i stil use p=nRT/V and integrate from vb to vc since T is constant here?) ok i just found that this part in parenthisis is correct - so my doubt is path A-B

Yes, the work done along ABC is ∫Pdv along the circular arc ABC. I don't see any need to break it up into AB and then BC. It won't be of much help to substitute P = nRT/V into the integral since T is not constant in the integration. However, you know from calculus that an integral is related to "area under the curve".

 

[WrongMan]

I'm not sure what "liquid heat" refers to. For part (b), I'm not sure what the path AC means. I guess it means the horizontal path from A to C. Not sure.

OK

You are not dealing with infinitesimal changes here. So, you should write ΔQ - ∫Pdv = ΔU.Yes, the work done along ABC is ∫Pdv along the circular arc ABC. I don't see any need to break it up into AB and then BC. It won't be of much help to substitute P = nRT/V into the integral since T is not constant in the integration. However, you know from calculus that an integral is related to "area under the curve".

thank you for your continued support
-yes A-C is the straight line A-C
-i meant substitute in nRT/V for the B-C part (T is constant)

Ok so since the cycle is symetric in relation to line AC i can say that the work done is half of what i calculated when i first presented this problem then i just substitute it into ΔQ - ∫Pdv = ΔU solve for Q.

- new question is there a way of finding work and heat just for AB (without using area under curve)?

 

[TSny]

-yes A-C is the straight line A-C

OK, good.

-i meant substitute in nRT/V for the B-C part (T is constant)

Even though states B and C have the same temperature, the intermediate states along the circular arc from B to C do not have the same temperature. So, you cannot treat T as a constant in the integration.

Ok so since the cycle is symetric in relation to line AC i can say that the work done is half of what i calculated when i first presented this problem

No, the work done along arc ABC is the area under the arc that extends from the arc all the way down to the V axis. So, it is not half the area of the circular cycle.

then i just substitute it into ΔQ - ∫Pdv = ΔU solve for Q.

Yes.

- new question is there a way of finding work and heat just for AB (without using area under curve)?

The only way that I can see to get the work for AB is using W = ∫PdV. The easiest way to get the value of the integral in this problem is to find the area. But, you could also use the fact that the path is along a circle to find an expression for P as a function of V. Then substitute for P in ∫PdV and do the integral. But that takes more work effort than just finding the area.

 

[WrongMan]

ok so i guess this is solved then. thank you!