Three charges arranged in equilateral triangle

[FlipStyle1308]

The three charges are held in place below. L = 1.40 m.

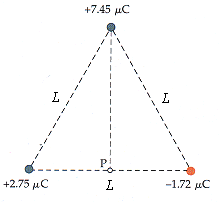
(a) Find the electric potential at point P.
(b) Suppose that a fourth charge, with a charge of 6.73 μC and a mass of 4.71 g, is released from rest at point P. What is the speed of the fourth charge when it has moved infinitely far away from the other three charges?

For part (a), I am pretty sure that I use the equation U = kqoq/r, but don't know what to do next.

 

[Dr Transport]

I would start by calculating the electric field at P (remember that the electric field is a vector so you need the vector form) from there you should be able to do the problem.

 

[FlipStyle1308]

So I use E = - V/r, right? How do I calculate this? I have to add values based on each charge, right? I don't know how to do this.

 

[Chronos]

The geometry is deafening. Think 1/r^2.

 

[FlipStyle1308]

Does this mean E = -V/r^2?

 

[FlipStyle1308]

Bump! I just correctly calculated the electric potential at point P to be 68.482 kV. How do I solve part (b)?

 

[FlipStyle1308]

I'm still stuck, is anyone able to help me figure out this last part of the question? Thanks.

 

[Tomsk]

If you know the potential at P, then you know the fourth charge's PE at P. You also know V at infinity, then use conservation of energy.

 

[FlipStyle1308]

So the electric potential at point P = (1/2)mv^2, v = 5392.538 m/s? Do I need to incorporate the 6.73 x 10^-6 C at all?

 

[Tomsk]

Yes, the potential energy is given by PE=qV.Then set that equal to 1/2 mv^2. Sorry if I wasn't clear on that.

 

[FlipStyle1308]

Okay, thanks!

 

[Chronos]

As Tomsk pointed out, establishing the global energy potential is the right place to start. It's all about entropy. Good explanation Tomsk. This is the guiding principle in almost all physics problems - define the boundary conditions.