- #1
paulimerci
- 287
- 47
- Homework Statement
- Question is posted below.
- Relevant Equations
- Coulomb law F_e = kq1q2/r^2
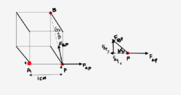
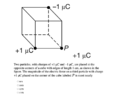
There are three charges with +1 μC and −1 μC, are placed at the opposite corners of a cube with edges of length 1 cm, and the distance from P to B is 1cm 2. I labeled them as A, P, and B, which is shown in the diagram below. Since we need to find the magnitude of the charge at point P and the charge at point P is +1 μC, it exerts an attractive force on point B and a repulsive force on point A. I've indicated the FBD below. Using Coulomb's law, we get
Fe=kq1q2r2
∑Fx=FBPcos45+FAP
∑Fx=91
∑Fy=FBPsin45
∑Fy=45.5N
Using Pythagorean we get,
Resultant magnitude of electric force = 101.7N
I did something wrong here. Can anyone point out where I made the mistake?
Thank you!
Fe=kq1q2r2
∑Fx=FBPcos45+FAP
∑Fx=91
∑Fy=FBPsin45
∑Fy=45.5N
Using Pythagorean we get,
Resultant magnitude of electric force = 101.7N
I did something wrong here. Can anyone point out where I made the mistake?
Thank you!
Attachments
Last edited: