Time Dependent Sinusoidal Perturbation Energy Conservation

[Samama Fahim]

The transition probability -- the probability that a particle which started out in the state $\psi_a$ will be found, at time $t$, in the state $\psi_b$ -- is

$$P_{a \to b} = \frac{|V_{ab}|}{\hbar^2} \frac{sin^2[(\omega_0 - \omega)t/2]}{(\omega_0 - \omega^2}.$$

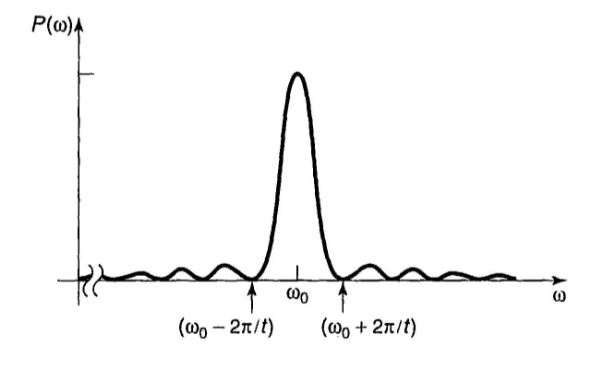
(Griffiths, Introduction to QM, p. 346)

Questions:
1) Does $P_{a \to b}$ represent transition probability or transition probability density? In the figure above, $P$ is plotted as a function of driving frequency. If $P(\omega)$ represents probability density (i.e. probability per unit frequency interval) then the area under this curve should be the total probability. Otherwise, the plot just gives us probabilities for transitions between the fixed states $a$ and $b$ for different sinusoidal perturbation frequencies $\omega$. Which is correct?

2) From the figure we can see that there is a non-zero transition probability for driving frequencies not equal to $\omega_0$. This would correspond, for example, to photons having energies less than $\hbar \omega_0$ provoking transitions that require energy $\hbar \omega_0$. Why is that?

 

[vanhees71]

The formula should read
$$P_{a \rightarrow b}=\frac{|V_{ab}|^2}{\hbar^2} \frac{\sin^2[(\omega-\omega_0) t]}{(\omega-\omega_0)^2}.$$
It is the transition probability at time $t$ to find the system in the energy eigenstate $b$ (of the unperturbed system) when it was in energy eigenstate $a$ at time $t=0$.

Energy is not conserved here, because the perturbation is time dependent. Thus there's some probability for transitions where $\omega \neq \omega_0$, but note that for $t \rightarrow \infty$ you'll get a corresponding energy-conserving $\delta$ distribution. That then describes, with the correct adiabatic-switching regulator applied, the transition rate (!) (average transition probability per unit time) for transitions between asymptotic free states, where the perturbative interaction is switched on and off adiabatically.

 

[Samama Fahim]

The formula should read
$$P_{a \rightarrow b}=\frac{|V_{ab}|^2}{\hbar^2} \frac{\sin^2[(\omega-\omega_0) t]}{(\omega-\omega_0)^2}.$$
It is the transition probability at time $t$ to find the system in the energy eigenstate $b$ (of the unperturbed system) when it was in energy eigenstate $a$ at time $t=0$.

Energy is not conserved here, because the perturbation is time dependent. Thus there's some probability for transitions where $\omega \neq \omega_0$, but note that for $t \rightarrow \infty$ you'll get a corresponding energy-conserving $\delta$ distribution. That then describes, with the correct adiabatic-switching regulator applied, the transition rate (!) (average transition probability per unit time) for transitions between asymptotic free states, where the perturbative interaction is switched on and off adiabatically.

Does this formula give the probability for transition between fixed states $a$ and $b$?

 

[vanhees71]

Yes.

 

[Samama Fahim]

The formula should read
$$P_{a \rightarrow b}=\frac{|V_{ab}|^2}{\hbar^2} \frac{\sin^2[(\omega-\omega_0) t]}{(\omega-\omega_0)^2}.$$
It is the transition probability at time $t$ to find the system in the energy eigenstate $b$ (of the unperturbed system) when it was in energy eigenstate $a$ at time $t=0$.

Energy is not conserved here, because the perturbation is time dependent. Thus there's some probability for transitions where $\omega \neq \omega_0$, but note that for $t \rightarrow \infty$ you'll get a corresponding energy-conserving $\delta$ distribution. That then describes, with the correct adiabatic-switching regulator applied, the transition rate (!) (average transition probability per unit time) for transitions between asymptotic free states, where the perturbative interaction is switched on and off adiabatically.

Maybe if the electron gets energy $\hbar \omega < \hbar \omega_0$ for a long time, it is able to make the transition from $a$ to $b$. Is that why the probability for such transitions is non-zero?

 

[Samama Fahim]

The formula should read
$$P_{a \rightarrow b}=\frac{|V_{ab}|^2}{\hbar^2} \frac{\sin^2[(\omega-\omega_0) t]}{(\omega-\omega_0)^2}.$$
It is the transition probability at time $t$ to find the system in the energy eigenstate $b$ (of the unperturbed system) when it was in energy eigenstate $a$ at time $t=0$.

Energy is not conserved here, because the perturbation is time dependent. Thus there's some probability for transitions where $\omega \neq \omega_0$, but note that for $t \rightarrow \infty$ you'll get a corresponding energy-conserving $\delta$ distribution. That then describes, with the correct adiabatic-switching regulator applied, the transition rate (!) (average transition probability per unit time) for transitions between asymptotic free states, where the perturbative interaction is switched on and off adiabatically.

The problem here is not whether the Hamiltonian is conserved. How is it possible for photons of energy less than the energy between the states $a$ and $b$ to provoke transitions between these states?

 

[DrDu]

Even if the frequency for t>0 is fixed, if you do a Fourier transform of the whole time dependence of the electric field, it will contain all frequencies. You simply don't have monochromatic photons, if the wavetrain is not infinitely long.

 

[Samama Fahim]

Even if the frequency for t>0 is fixed, if you do a Fourier transform of the whole time dependence of the electric field, it will contain all frequencies. You simply don't have monochromatic photons, if the wavetrain is not infinitely long.

The plot shows how $P(\omega)$, i.e., the probability of transition from a fixed state $a$ to a fixed state $b$ changes with $\omega$, the driving frequency. If that is correct, then it should be possible for a given driving frequency $\omega < \omega_0$ to provoke a transition between the states $a$ and $b$, which would require $\hbar \omega_0$. But as you say, even this $\omega < \omega_0$ can be "broken up" into all sorts of frequencies that will provide the required transition energy $\hbar \omega_0$. Is that correct?