Time evolution of an expectation value

[jaurandt]

Watching Dr. Susskind show how to find the time evolution of the average of an observable K, he writes:

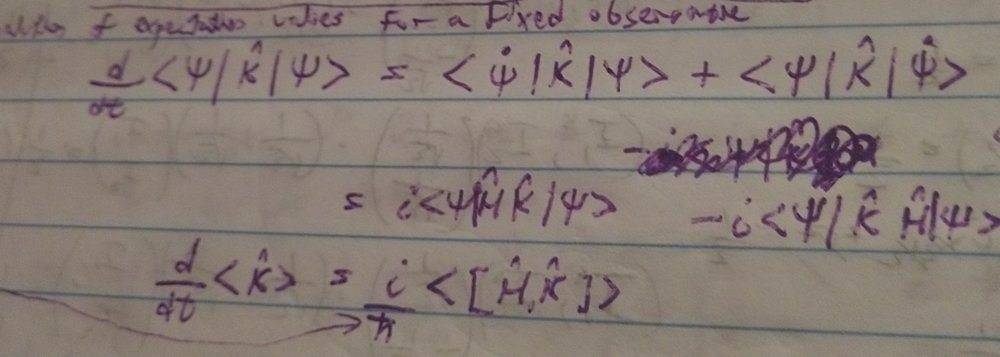
I can not for the life of me figure out he derived it, and he also did something which I found terribly annoying throughout which is set hbar to 1, so after steps you lose where the hbar goes. Can anyone help me figure out how this is derived?

 

[A. Neumaier]

Apply on the left the product rule twice and use twice the Schrödinger equation $i\hbar \partial_t \psi = \widehat H \psi$.

 

[jaurandt]

Apply on the left the product rule twice and use twice the Schrödinger equation $i\hbar \partial_t \psi = \widehat H \psi$.

Thanks for your reply. That much I do understand, but what I don't understand is how doing that could ever produce a -i since H is obviously Hermitian and can act on either side...

 

[Orodruin]

Setting $\hbar = c = 1$ is standard unit convention in high-energy physics. It is just a matter of what unit system you choose to work in and natural units are by far the most convenient. You can always go back to a unit system where this is not the case by using dimensional analysis to insert the appropriate powers of $\hbar$ and $c$.

 

[A. Neumaier]

Thanks for your reply. That much I do understand, but what I don't understand is how doing that could ever produce a -i since H is obviously Hermitian and can act on either side...

But bras are conjugated, hence on the bra side, $1/i=-i$ becomes $i$.

 

[jaurandt]

But bras are conjugated, hence on the bra side, $1/i=-i$ becomes $i$.

So I am wrong in saying
(i)(hbar)d/dt<psi| = <psi|H ? I'm sorry I'm brand new to this forum and I don't know how to create the symbols.

 

[jaurandt]

Setting $\hbar = c = 1$ is standard unit convention in high-energy physics. It is just a matter of what unit system you choose to work in and natural units are by far the most convenient. You can always go back to a unit system where this is not the case by using dimensional analysis to insert the appropriate powers of $\hbar$ and $c$.

Maybe it'll come more naturally to me eventually, but dimensional analysis seems to confuse me more than just leaving in the constants.

 

[A. Neumaier]

I don't know how to create the symbols.

Use standard latex but with two hash signs in place of single dollars (but keep double dollars). You can look at how I did it by clicking on the reply button of my post.

So I am wrong in saying(i)(hbar)d/dt<psi| = <psi|H ?

Yes. It is easiest to see if you use linear algebra notation, i.e., $\psi=|\psi\rangle$ (viewed as a column vector) and $\psi^*=\langle\psi|$ (viewed as the conjugate transposed row vector). Then $$i\hbar \partial_t \psi^*=-(i\hbar \partial_t \psi)^*=-(H\psi)^*=-\psi^*H.$$

 

[Orodruin]

Maybe it'll come more naturally to me eventually, but dimensional analysis seems to confuse me more than just leaving in the constants.

After getting used to it, leaving the constants will just annoy you to the extreme as they add nothing of value to the physics and just act to obscure the mathematical relationships.

 

[A. Neumaier]

After getting used to it, leaving the constants will just annoy you to the extreme as they add nothing of value to the physics and just act to obscure the mathematical relationships.

I don't agree. After 28 years of doing quantum mechanics I still like to write them each time (and am pleased if others do so, too). It displays the classical limit $\hbar\to 0$ and the nonrelativistic limit $c^{-1}\to 0$ very naturally. Writing $\iota:=i/\hbar$ and $x_0=ct$ in the formulas is almost as easy as writing $i$ and $x_0=t$ preserves the units.

 

[Orodruin]

I don't agree. After 28 years of doing quantum mechanics I still like to write them each time (and am pleased if others do so, too). It displays the classical limit $\hbar\to 0$ and the nonrelativistic limit $c^{-1}\to 0$ very naturally. Writing $\iota:=i/\hbar$ and $x_0=ct$ in the formulas is almost as easy as writing $i$ and $x_0=t$ preserves the units.

To each his (or her) own. To me, it is just clutter. Typically the non-relativistic and classical limits can be considered in other ways that do not involve $c$ or $\hbar$ and are more physical. Using $c$ or $\hbar$ is just a proxy.

 

[jaurandt]

Use standard latex but with two hash signs in place of single dollars (but keep double dollars). You can look at how I did it by clicking on the reply button of my post.

Yes. It is easiest to see if you use linear algebra notation, i.e., $\psi=|\psi\rangle$ (viewed as a column vector) and $\psi^*=\langle\psi|$ (viewed as the conjugate transposed row vector). Then $$i\hbar \partial_t \psi^*=-(i\hbar \partial_t \psi)^*=-(H\psi)^*=-\psi^*H.$$

First of all, I agree with your most recent posts about the constants. And I just started my own course of study on QM about 2 months ago. Very rigorously I may add, as I spend almost all of my time doing it.

Second, your math implies that the adjoint of $$\partial_t$$ is $$\partial_t$$

Is this correct? Basically, I just wasn't conjugating i for the bra form? In other words

H|psi> = (i)(hbar)(d/dt)|psi>

Corresponds to

<psi|H = <psi|(d/dt)(hbar)(-i)

Is this correct?

 

[A. Neumaier]

Your math implies that the adjoint of $$\partial_t$$ is $$\partial_t$$

Is this correct?

No. $\partial_t$ is not an operator acting on the Hilbert space but on the t-dependence of the state. Its adjoint is not defined in this context.