Time evolution of the electromagnetic wavefunction on a lattice

[James1238765]

TL;DR

Why does this time evolution of the electromagnetic wavefunction diverges?

The Maxwell wavefunction of a photon is given in [here] as follows:

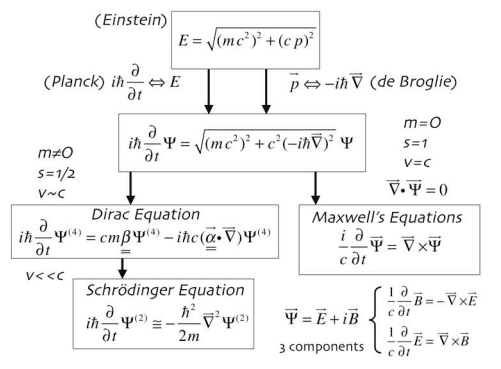
Because the curl operation mixes 3 different components, this wavefunction only works for a minimum of 3 space dimensions, with each grid point having 6 component numbers ${E^1, E^2, E^3, B^1, B^2, B^3}$, and with the following update rules:

$$ E_{x,y,z}^1 = E_{x,y,z}^1 + B_{x,y+1,z}^3 - B_{x,y,z}^3 - B_{x,y,z+1}^2 + B_{x,y,z}^2$$
$$ E_{x,y,z}^2 = E_{x,y,z}^2 + B_{x,y,z+1}^1 - B_{x,y,z}^1 - B_{x+1,y,z}^3 + B_{x,y,z}^3$$
$$ E_{x,y,z}^3 = E_{x,y,z}^3 + B_{x+1,y,z}^2 - B_{x,y,z}^2 - B_{x,y+1,z}^1 + B_{x,y,z}^1$$
$$ B_{x,y,z}^1 = B_{x,y,z}^1 - E_{x,y+1,z}^3 + E_{x,y,z}^3 + E_{x,y,z+1}^2 - E_{x,y,z}^2$$
$$ B_{x,y,z}^2 = B_{x,y,z}^2 - E_{x,y,z+1}^1 + E_{x,y,z}^1 + E_{x+1,y,z}^3 - E_{x,y,z}^3$$
$$ B_{x,y,z}^3 = B_{x,y,z}^3 - E_{x+1,y,z}^2 + E_{x,y,z}^2 + E_{x,y+1,z}^1 - E_{x,y,z}^1$$

corresponding to $\frac{dE}{dt} = \nabla x B$ and $\frac{dB}{dt} = - \nabla x E$

The complicated time evolution due to the mixing of the 6 components over time gives rise to complex behavior, which are not intuitive to predict.

1.
Setting E1 = 1 over all $[x,y,z]$ points in the 3 dimensional grid, and setting all other components E2, E3, B1, B2, B3 = 0 all over the grid, we obtain:

with no time evolution of any components throughout the grid.

2.
Setting E1 = $sin (\frac{x}{width}2\pi)$ over all [x,y,z] points in the grid, and setting all other components to 0, we obtain:

still without time evolution.

3.
Setting Ei = $sin (\frac{i}{width}2\pi)$ for all the 6 components:

still produces no time evolution! The curl operation is rather finicky.

4.
Setting E1 = $sin (\frac{x+y+z}{width}2\pi)$ and $E2, E3, E4, E5, E6 = 0$ everywhere:

finally produces a time evolution.

However the time evolution explodes partway, as shown in the chart, and the numerical data below.

I am unsure why this happens, because the update rules involve only additions (with no multiplications or other fancy operations)?

 

[Frabjous]

I have my doubts about the maxwell wavefunction of the photon idea, but for Maxwell’s equations just from poking around the web, people seem to use FDTD (also called Yee’s method) for the discretization which staggers E and H in time and space.

 

[James1238765]

@Frabjous thank you. i am interested in these multi-dimensional cross relationships between lattice grid components over time. In the 8-components Dirac equation, a similar looking complicated time evolution relationship also exists between the individual components.

Is there a name for the mathematical branch that can analyze the behavior over time of these kind of self interacting components?

 

[Frabjous]

Sorry, I have not been exposed to that. My generic advice is that these are really ugly equations to solve in general. You need to get specific about the problem you are trying to solve and then try to find a technique. As you discovered above, stability conditions can kill you.

 

[hutchphd]

I would call this finite element analysis. FYI.... Folks usually don't start by solving eight component fields in four+ dimensions. Perhaps a more measured approach would serve you better?

 

[James1238765]

@hutchphd I am familiar with the discretization and computation aspects using finite elements. Can finite elements methods also analyze for instance which initial conditions with be stable over time and which will not, *without doing the computation*? Can you link to which method in finite elements allows us to do this?

 

[hutchphd]

No I cannot. These are not easy and only rarely yield to clever analytic manipulation Nobel prizes have been sometimes involved.

 

[James1238765]

@hutchphd thank you. You seem to hint towards the Navier Stokes wave, so while at it I translated the usual equations into the same notation as above for future reference. There are 3 velocity component numbers $\{u, v, w\}$ in the 3 dimensional Navier Stokes grid $[x, y, z]$:

$$ \frac{du}{dt} = \frac{d^2u}{dx^2} + \frac{d^2u}{dy^2} + \frac{d^2u}{dz^2} - u\frac{du}{dx} - v\frac{du}{dy} - w\frac{du}{dz}$$
$$ \frac{dv}{dt} = \frac{d^2v}{dx^2} + \frac{d^2v}{dy^2} + \frac{d^2v}{dz^2} - u\frac{dv}{dx} - v\frac{dv}{dy} - w\frac{dv}{dz}$$
$$ \frac{dw}{dt} = \frac{d^2w}{dx^2} + \frac{d^2w}{dy^2} + \frac{d^2w}{dz^2} - u\frac{dw}{dx} - v\frac{dw}{dy} - w\frac{dw}{dz}$$

discretized into:

1. The u velocity component update:
$$\Phi_{x,y,z}^u = \Phi_{x,y,z}^u + \Phi_{x+1,y,z}^u - 2\Phi_{x,y,z}^u + \Phi_{x-1,y,z}^u + \Phi_{x,y+1,z}^u - 2\Phi_{x,y,z}^u + \Phi_{x,y-1,z}^u$$
$$+\Phi_{x,y,z+1}^u - 2\Phi_{x,y,z}^u + \Phi_{x,y,z-1}^u -\Phi_{x,y,z}^u (\Phi_{x+1,y,z}^u - \Phi_{x,y,z}^u) $$
$$-\Phi_{x,y,z}^v(\Phi_{x,y+1,z}^u - \Phi_{x,y,z}^u) -\Phi_{x,y,z}^w(\Phi_{x,y,z+1}^u - \Phi_{x,y,z}^u)$$

2. The v velocity component update:
$$\Phi_{x,y,z}^v = \Phi_{x,y,z}^v + \Phi_{x+1,y,z}^v - 2\Phi_{x,y,z}^v + \Phi_{x-1,y,z}^v +
\Phi_{x,y+1,z}^v - 2\Phi_{x,y,z}^v + \Phi_{x,y-1,z}^v$$
$$+\Phi_{x,y,z+1}^v - 2\Phi_{x,y,z}^v + \Phi_{x,y,z-1}^v -\Phi_{x,y,z}^u (\Phi_{x+1,y,z}^v - \Phi_{x,y,z}^v) $$
$$- \Phi_{x,y,z}^v(\Phi_{x,y+1,z}^v - \Phi_{x,y,z}^v) -\Phi_{x,y,z}^w(\Phi_{x,y,z+1}^v - \Phi_{x,y,z}^v)$$

3. The w velocity component update:
$$\Phi_{x,y,z}^w = \Phi_{x,y,z}^w + \Phi_{x+1,y,z}^w - 2\Phi_{x,y,z}^w + \Phi_{x-1,y,z}^w +\Phi_{x,y+1,z}^w - 2\Phi_{x,y,z}^w + \Phi_{x,y-1,z}^w $$
$$+\Phi_{x,y,z+1}^w - 2\Phi_{x,y,z}^w + \Phi_{x,y,z-1}^w -\Phi_{x,y,z}^u (\Phi_{x+1,y,z}^w - \Phi_{x,y,z}^w) $$
$$
-\Phi_{x,y,z}^v(\Phi_{x,y+1,z}^w - \Phi_{x,y,z}^w) -\Phi_{x,y,z}^w(\Phi_{x,y,z+1}^w - \Phi_{x,y,z}^w)$$

Yes, I can see the Nobels and Fields and Millennial Prizes lining up if anyone manages to analyze *that* thing.

 

[hutchphd]

No hint intended

 

[James1238765]

Here are a few resulting models based on the Navier Stokes wave:

1. The divergence encountered in the original post is likely due to known instability in the numerically computed

$$ \Phi_{x+1} - 2\Phi_{x} + \Phi_{x-1}$$

when done iteratively. An alternative method called Gauss-Seidel should be used to compute the same quantity.

2. A similar form of the Navier Stokes equations for density (in 2 dimensions) is:

$$ \frac{d\rho}{dt} = \frac{d^2\rho}{dx^2} + \frac{d^2\rho}{dy^2} - u\frac{d\rho}{dx} - v\frac{d\rho}{dy} + Source$$

Using only the diffusion part $\frac{d^2\rho}{dx^2} + \frac{d^2\rho}{dy^2}$, we obtain:

3. Adding adjection $- u\frac{d\rho}{dx} - v\frac{d\rho}{dy}$ to the previous model, we obtain:

4. Adding sources of density through $Source$ to the previous model, we obtain:

5. Adding nonlinear vector diffusion evolution to the velocity field, plus advection based on a secondary "velocity-of-velocity" field, plus external sources of velocity, in addition to as previously evolving the density field, we get:

A lot more modeling seems possible with familiarity and expertise in fluid modeling using Navier Stokes equations.

6. The Millennium Problem description for Navier Stokes seems to be about analytic solutions to the equations and their properties: