To find the centre of gravity of a lamina

[gnits]

Homework Statement

To find the centre of gravity of a lamina

Relevant Equations

Balancing of moments

Could I please ask for help with the following:

A lamina ABCD is in the form of a trapezium in which DC is parallel to AB, AB = 2a, CD = a and AD = h and the angle BAD is 90 degrees. Find the position of the centre of gravity of the lamina from the edges AD and AB.

The lamina is placed vertically with edge BC on a horizontal plane. Find the minimum value of h for the lamina to remain in this position without toppling in its own vertical plane.

I've done the first part and get the book answers of:

Center of gravity = ( 7a/9, 4h/9)

It's the second part where I am stuck.

Here's a diagram:

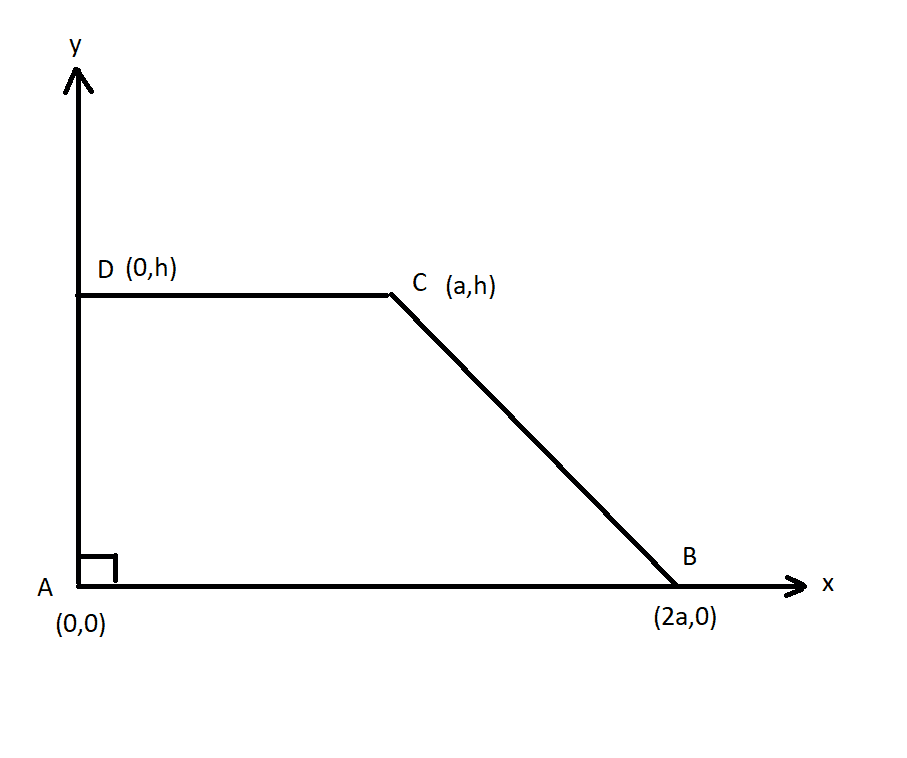
So I reasoned that the lamina would topple if h (= length AD) were reduced to a width where the centre of gravity were to fall on the line joining A to C, so that when resting on side BC the centre of gravity would then be above C.

Would that be correct?

But this leads to:

Equation of line joining A to C is y = hx/a

So if centre of gravity is on this line then the point (7a/9, 4h/9) should satisfy the equation. But this leads to:

4h/9 = 7a/9 * h/a

and all the values cancel.

Book's answer is a*sqrt(10)/5

Thanks for any help,
Mitch.

EDIT:

Alternative method. Here's a diagram of the rotated shape:

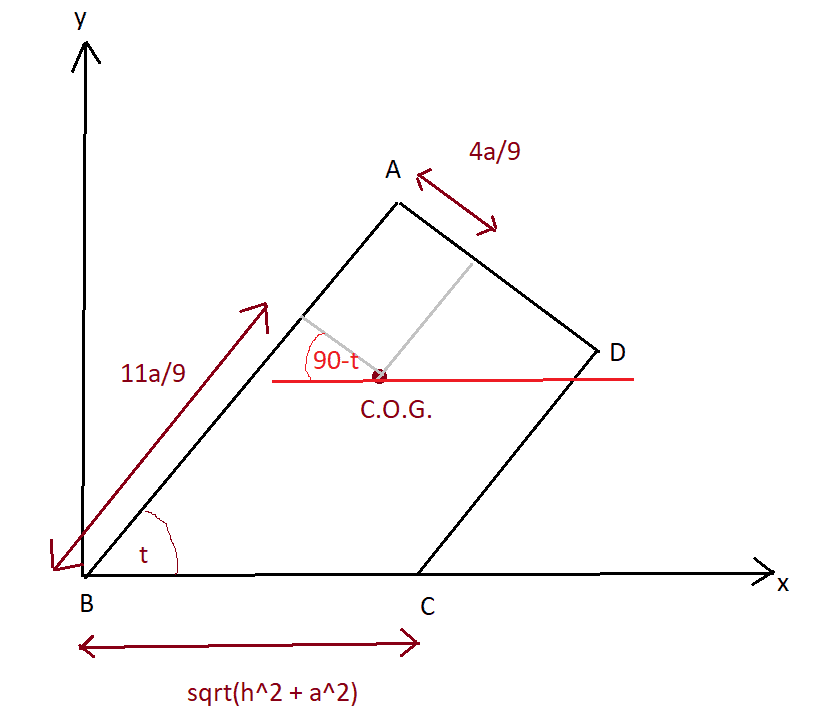
So condition for C.O.G. to be above C is:

(11a/9)*cos(t) + (4h/9)*sin(t) = sqrt(a^2+h^2)

and we know that cos(t) = a/(sqrt(a^2+h^2) and sin(t) = h/sqrt(a^2+h^2)

And this leads to the right answer.

So with my first attempt, what was my mistake of reasoning?

FURTHER EDIT: I think my first method implicitly assumes that the quadrilateral part of the trapezium is a square, which it need not be.

 

[Steve4Physics]

So I reasoned that the lamina would topple if h (= length AD) were reduced to a width where the centre of gravity were to fall on the line joining A to C, so that when resting on side BC the centre of gravity would then be above C.

Would that be correct?

No. With reference to your 2nd diagram, you can't assume AC is vertical at the critical (tipping) point.

I'll call the centre of gravity 'P' for brevity.

For stability, P must be above the base BC.

If P is slightly to the left of C (i.e. above BC) the weight produces an anticlockwise moment (torque) about C, This will be balanced by a clockwise moment produced by the normal reaction from the ground on BC, giving stability.

But if P is slightly to the right of C (i.e. outside BC) the weight produces a clockwise moment about C - which can't be balanced. So the lamina topples (rotates clockwise about C).

If you consider the traingle PBC, you want P vertically above C so BPC is a right-triangle with ∠BCP = 90º.

 

[gnits]

Thanks very much for you help. Much appreciated.