To find the time for which a vessel is within range of these guns

[gnits]

Homework Statement

To find the time for which a vessel is in range of guns

Relevant Equations

d=st

Could I please ask for help with the following question (the second part):

A cruiser sailing due north at 24 km/h sights a destroyer 48 km due east sailiing at 56 km/h on a course (360-a) degress where cos(a)=11/14.

Show that the destroyer's course realtive to the cruiser is on a bearing of 300 degrees and find the relative speed.

If the cruiser's guns have a maximum reange of 30 km and both ships maintain course and speed, find for how long the destoyer will be within range.

I've done the first part and agree with the book's answer:

Let $V_{DC}$ be the velocity of the destroyer realtive to the cruiser then my (and the book's) answer is:

$V_{DC_x}=-20\sqrt{3}$ and $V_{DC_y}=20$

So, here's my answer to the second part and I disagree with the book answer of 56 minutes.

Let $r_C$ be the position vector of the cruiser and $r_D$ be the position vector of the destroyer, both relative to the cruiser's starting position, then:

(let i be the unit vector in the direction of east and j the unit vector in the direction of north and t be time)

$r_C=24tj$ and $r_D=(48-20\sqrt{3}t)i+20tj$

and so the position vector of the destroyer relative to the cruiser is:

$r_{DC}=(48-20\sqrt{3}t)i-4j$

And so the square of the distance between the vessels is:

$D^2=(48-20\sqrt{3}t)^2+16t^2$

And so we need to solve:

$(48-20\sqrt{3}t)^2+16t^2 <900$

To check, I put this into Wolfram Alpha and get:

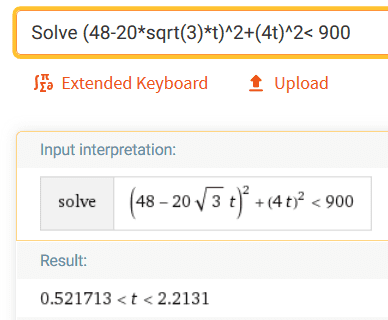
And that gives a time of approx 2.21 - 0.52 = 1.69 hours which is not the book answer,

Can anyone show me my mistake?

Thanks,
Mitch.

 

[jbriggs444]

Is the destroyer moving at 4 km/h north/south relative to the cruiser or 20 km/h? You have equations that say both.

 

[etotheipi]

It might also be easier to solve the second part by drawing a diagram and considering an isosceles triangle, it just means you can substitute some of the long-winded algebra for a bit of geometry.

 

[gnits]

Thanks for your comments,

I found my silly mistake right at the beginning. I used the relative velocity of the deatroyer rather than its velocity relative to the Earth in my position vector equations.

 

[etotheipi]

Thanks for your comments,

I found my silly mistake right at the beginning. I used the relative velocity of the deatroyer rather than its velocity relative to the Earth in my position vector equations.

You could also done it all in the frame of the cruiser and worked it through that way. But yeah, it's an easy mistake (but wrong!) to mix and match frames.