COCoNuT
- 35
- 0
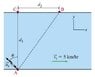
A swimmer wants to cross a river, from point A to point B. The distance d_1 (from A to C) is 200 m, the distance d_2 (from C to B) is 1500 m, and the speed V_r of the current in the river is 5 km/h. Suppose that the swimmer makes an angle of 45 degrees(0.785 radians) with respect to the line from A to C, as indicated in the figure.
Question #1) To swim directly from A to B, what speed U_s, relative to the water, should the swimmer have? Express the swimmer's speed numerically, to three significant figures, in units of kilometers per hour.
U_s[/tex] = __________km/h
ok here's what i think i should do. first i need to find the distance from A to B. so of course a^2 + b^2 = c^2
1500^2 + 200^2 = C^2
C= 1513.37m from distance A to B
ok i know that it makes a 45 degrees angle with respect to the line from A to C. and the inner angle(dont know the math term) or the angle next to it is also 45 degrees(90-45).
that means i can find the initial velocity of Vx and Vy.
have to convert meters to km first right? so 1500 would be 1.5
Vx = 1.5km*cos(45) = 1.06 km/h
Vy = .2km*sin(45) = .1414 km/h
ok so i know the distance from A to B, the Vx and Vy initial velocities. I am stuck here, don't know what else to do. the picture is attached.
Question #1) To swim directly from A to B, what speed U_s, relative to the water, should the swimmer have? Express the swimmer's speed numerically, to three significant figures, in units of kilometers per hour.
U_s[/tex] = __________km/h
ok here's what i think i should do. first i need to find the distance from A to B. so of course a^2 + b^2 = c^2
1500^2 + 200^2 = C^2
C= 1513.37m from distance A to B
ok i know that it makes a 45 degrees angle with respect to the line from A to C. and the inner angle(dont know the math term) or the angle next to it is also 45 degrees(90-45).
that means i can find the initial velocity of Vx and Vy.
have to convert meters to km first right? so 1500 would be 1.5
Vx = 1.5km*cos(45) = 1.06 km/h
Vy = .2km*sin(45) = .1414 km/h
ok so i know the distance from A to B, the Vx and Vy initial velocities. I am stuck here, don't know what else to do. the picture is attached.
Attachments
Last edited: