Problem using vectors and relative motion

[Hema]

Homework Statement

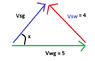
A river of width 4 km flows at 5 km/h. A swimmer whose speed relative to water is 4 km/h, starts swimming from a point A on a bank. What minimum distance will the swimmer have to walk on the other bank to reach point B directly opposite to A?
[/B]

Homework Equations

Vba = Vb - Va is the equation for relative velocity

The Attempt at a Solution

Let Vwg be absolute velocity of river (vector), Vsw be relative velocity of swimmer wrt river (vector) and Vsg be absolute velocity of swimmer wrt ground (vector). Now I know that
Vsg = Vwg + Vsw
but what angles do the vectors make? I would have supposed that the swimmer makes his strokes at right angles to the river current and therefore the vectors form a right triangle with Vsw perpendicular to Vwg and therefore Vsg will be the hypotenuse, but the answer for the value of Vsq is 3 and this would not follow Pythagoras theorem. What angles do the vectors make then? How do I do this?
[/B]

 

[BvU]

Hello Hema,

I would have supposed that the swimmer makes his strokes at right angles to the river current

It is a pity you already have the answer and know that what you get with your assumption is not it. As Sherlock would say 'then the assumption is wrong'. Why would it be wrong ?

This is a minimization problem. Did you learn about those recently ?

 

[Hema]

Hello Hema,
It is a pity you already have the answer and know that what you get with your assumption is not it. As Sherlock would say 'then the assumption is wrong'. Why would it be wrong ?

This is a minimization problem. Did you learn about those recently ?

What is a minimization problem? No, I don't think I have learned them. I have only studied a few relative velocity of swimmer type problems. Yes, you are right, I suppose my assumption is wrong. But the only other way for this to follow Pythagoras theorem is for Vsw to be perpendicular to Vsg, but that doesn't seem to make sense..

 

[BvU]

Ok, so we try to do this with geometry and not with the algebraical approach.
Note that the aim is not: to get across as fast as possible.
If the swimmer would swim against the stream, he would lose 1 km/h and never get across.
At right angles he crosses in 1 h and loses 5 km.
He can reduce the loss and do something in between . Make a few sketches...

 

[Hema]

Ok, so we try to do this with geometry and not with the algebraical approach.
Note that the aim is not: to get across as fast as possible.
If the swimmer would swim against the stream, he would lose 1 km/h and never get across.
At right angles he crosses in 1 h and loses 5 km.
He can reduce the loss and do something in between . Make a few sketches...

This is the result I get.. for horizontal distance traveled on opposite bank to be minimum component of Vsg must be minimum along horizontal.. which will be when cos x = 0 or x is a right angle.. but in that case Vsw will be hypotenuse.. where did I go wrong?

 

[BvU]

Who says you are wrong ? You did not yet calculate how far he has to walk on the other side

 

[Hema]

Who says you are wrong ? You did not yet calculate how far he has to walk on the other side

But is x is 90 degrees he doesn't have to walk across right? He can just reach the opposite side- he won't be drifting at all

 

[BvU]

That's right. What speed would he need for $x = {\pi\over 2}$ ?

 

[Hema]

That's right. What speed would he need for $x = {\pi\over 2}$ ?

It is not possible for x to be 90 degrees right? In that case 4 would be the hypotenuse and 5 one of the sides, which is not possible as the hypotenuse is always longest. I'm so sorry for the late reply by the way, something went wrong with my internet connection.

 

[BvU]

That's correct. He would need more than 5 and only has 4 km/h.
Now use the angle at the lower right (or it's sine) to calculate how far he has to walk. You already know he has to walk 5 km if $\sin \alpha = 1$

 

[Hema]

That's correct. He would need more than 5 and only has 4 km/h.
Now use the angle at the lower right (or it's sine) to calculate how far he has to walk. You already know he has to walk 5 km if $\sin \alpha = 1$

If Vwg is the hypotenuse then I suppose Vsq would be 3, and the component would be 3 * cos x = 12/5.. but it can have many other values as well right?

 

[BvU]

I have no idea what you mean with Vsq. Did you mention if before ? Ah, but without telling what it is ... otherwise you probably would have been informed that it is NOT the resultant speed along the river.

Now use the angle at the lower right (or it's sine) to calculate how far he has to walk.

Did I propose nonsense ? Or did you miss this 'hint'?

 

[Hema]

I have no idea what you mean with Vsq. Did you mention if before ? Ah, but without telling what it is ... otherwise you probably would have been informed that it is NOT the resultant speed along the river.
Did I propose nonsense ? Or did you miss this 'hint'?

I tried it again and got it, thanks for your help!