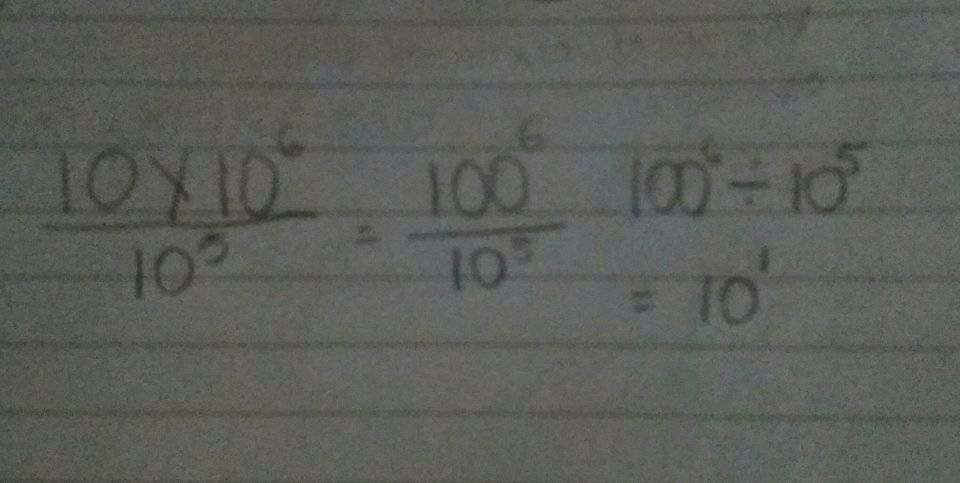SUMMARY
The discussion focuses on the mathematical principle that when multiplying powers with the same base, the exponents are added, as expressed in the formula 10^m × 10^n = 10^{m+n}. Participants clarify that 10 × 10^6 equals 10^7, not 100^6. The importance of the order of operations, specifically the PEMDAS/BEDMAS rules, is emphasized to avoid common mistakes in calculations involving exponents and multiplication. Additionally, the concept of negative exponents is introduced, reinforcing the understanding of division in terms of subtraction of exponents.
PREREQUISITES
- Understanding of exponentiation rules, specifically
10^m × 10^n = 10^{m+n}
- Familiarity with the order of operations (PEMDAS/BEDMAS)
- Basic knowledge of negative exponents and their implications
- Ability to perform longhand calculations with powers of ten
NEXT STEPS
- Study the properties of exponents, including negative and zero exponents
- Practice problems involving multiplication and division of powers with the same base
- Explore the applications of scientific notation in real-world contexts
- Learn about logarithms and their relationship to exponents
USEFUL FOR
Students, educators, and anyone looking to strengthen their understanding of exponentiation and its applications in mathematics and science.