SUMMARY
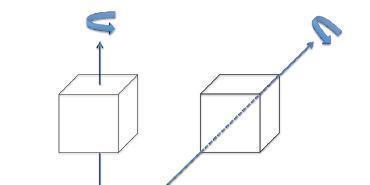
The discussion centers on determining which of two cubes has a larger moment of inertia. Participants agree that the cube on the right has a larger moment of inertia due to its rotation not being around the principal axes that pass through the center of mass. The relevant equation for calculating moment of inertia is highlighted, emphasizing that it can be derived from the parallel axis theorem, although some participants suggest avoiding its use in this context. Calculating the moment of inertia tensor is recommended for deeper understanding.
PREREQUISITES
- Understanding of moment of inertia and its significance in rotational dynamics
- Familiarity with the parallel axis theorem and its applications
- Knowledge of integral calculus for evaluating moment of inertia
- Basic concepts of principal axes and their relation to mass distribution
NEXT STEPS
- Calculate the moment of inertia for both cubes using the standard definition
- Explore the moment of inertia tensor for various shapes
- Learn about the implications of the parallel axis theorem in different scenarios
- Investigate the moment of inertia for a flat rectangular sheet in both straight and diagonal orientations
USEFUL FOR
Students and professionals in physics, mechanical engineering, and materials science who are studying rotational dynamics and moment of inertia calculations.