Torque on a dipole near a infinite conducting plane

[Pushoam]

Homework Statement

Homework Equations

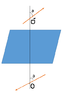
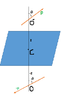
3. The Attempt at a Solution [/B]

I have drawn this diagram using MS paint, could you please tell me some other software in which I can draw and insert greek symbols, too ?Let me take the origin at O.
$\hat r \left(\alpha\right) ≡ \hat r\text{ at angle }\alpha ~with ~z - axis$
Considering the image problem,
$\vec E \left (O' \right)$ due to the image dipole $= \frac { -kp} { {2 z}^3 } \left( 2 \cos \alpha ~ \hat r \left( \theta = 0 \right) + \sin \alpha ~ \hat \theta \left ( \theta =0 \right) \right )$
$\\ \hat r = \sin \theta ~ \hat s + \cos \theta ~ \hat z \\ \hat \theta = - \sin \theta ~ \hat z +\cos \theta ~ \hat s \\\text { at } \theta =0, ~ \hat r = \hat z ~ and ~ \hat \theta = \hat s \\ \\ \vec p = p~ \hat r \left ( \alpha \right)$

Now,
torque $\vec N = \vec p \times \vec E$

$= p ~ \hat r$ $\left( \alpha \right ) \times$ $\frac { -kp} { {2z}^3 } \left( 2 \cos \alpha ~ \hat r \left( \theta = 0 \right) + \sin \alpha ~ \hat \theta \left ( \theta =0 \right) \right)$

$\\ = p \hat r\left( \alpha \right ) \times \frac { -kp} {{2z}^3 } \left( 2 \cos \alpha ~\hat z + \sin \alpha ~ \hat s \right)$

$= \frac {-kp^2}{ \left (2z\right) ^3 } \left[ - 2 \cos \alpha \sin \alpha ~\hat \phi + \cos \alpha \sin \alpha ~ \hat \phi \right ]$

$\\ = \frac {kp^2}{16 z ^3 } \sin \alpha ~ \hat \phi$

To answer the final part,
I guess the orientation of plane is x-y and $\hat \phi$ is also in the x-y orientation. So, the dipole will come to rest in the orientation which is parallel to the plane .
But why will it come to rest? Why won't it oscillate (as there are no other net force acting on the dipole)?

 

[TSny]

I had a difficult time following all of your unit vector notations. I believe your unit vector $\hat{s}$ could be called the "radial polar unit vector" in cylindrical coordinates.

Considering the image problem,
$\vec E \left (O' \right)$ due to the image dipole $= \frac { -kp} { {2 z}^3 } \left( 2 \cos \alpha ~ \hat r \left( \theta = 0 \right) + \sin \alpha ~ \hat \theta \left ( \theta =0 \right) \right )$

Are you sure both terms in the parentheses are positive? There should be a set of parentheses in the denominator (which you finally put in near the very end of your calculation.)

$\\ = \frac {kp^2}{16 z ^3 } \sin \alpha ~ \hat \phi$

Did you mean to type $2 \alpha$ for the argument of the sine function? I don't get the same numerical factor out front due to the possible sign error that I mentioned above.

To answer the final part,
I guess the orientation of plane is x-y and $\hat \phi$ is also in the x-y orientation. So, the dipole will come to rest in the orientation which is parallel to the plane .
But why will it come to rest? Why won't it oscillate (as there are no other net force acting on the dipole)?

Yes, it would oscillate. I guess they want you to assume small damping so that it comes to rest at the equilibrium position. I agree that the equilibrium position would be parallel to the conducting plane.

 

[Pushoam]

Are you sure both terms in the parentheses are positive?

$\vec E$ due to an ideal dipole \vec p at a point $\hat r \left( \theta \right )$ is given by

Here, r = 2z
$\theta = \alpha$
The electric field at O' due to p $= \frac { kp} { \{2 z\}^3 } \left( 2 \cos \alpha ~ \hat r \left( \theta = 0 \right) + \sin \alpha ~ \hat \theta \left ( \theta =0 \right) \right )$
So, The electric field at O' due to -p $= \frac { -kp} { \{2 z\}^3 } \left( 2 \cos \alpha ~ \hat r \left( \theta = 0 \right) + \sin \alpha ~ \hat \theta \left ( \theta =0 \right) \right )$

Is there anything wrong with it?

 

[TSny]

$\vec E$ due to an ideal dipole \vec p at a point $\hat r \left( \theta \right )$ is given by

View attachment 208392

Now you're using spherical coordinates.

Here, r = 2z
$\theta = \alpha$
The electric field at O' due to p $= \frac { kp} { \{2 z\}^3 } \left( 2 \cos \alpha ~ \hat r \left( \theta = 0 \right) + \sin \alpha ~ \hat \theta \left ( \theta =0 \right) \right )$

This is confusing. You say $\theta = \alpha$ but then you say $\theta = 0$ and $\alpha \neq 0$.

There is a nice way to write the electric field of a dipole that is independent of coordinate system. See equation 13 here:
http://phys.columbia.edu/~nicolis/Dipole_electric_field.pdf

You can apply this expression to any coordinate system that you find convenient. Thus, you can apply it to this picture to find E at O' in terms of unit vectors $\hat y$ and $\hat z$.

You can then switch the sign of E to correspond to p pointing in the opposite direction to that shown in this picture.

 

[Pushoam]

$\vec N = \vec p \left ( ~at ~ O' \right ) \times \{$ ${\vec E \left ( ~at ~ O' \right )} = { \frac k { \{ 2 z \}^3 } }$ $\left [ 3 { \left ( - \vec p ⋅ \hat z \right ) \hat z } +\vec p \right ]$ $\}$
$\\ = \frac {- 3 k p^2} { \{ 2 z \}^3 } \cos \alpha \{ \vec p \times \hat z\} \\ = \frac {- 3 k p^2} {16 z^3} \sin 2 \alpha \{- \hat \phi \}$

I agree that the equilibrium position would be parallel to the conducting plane.

The book's solution says that the equilibrium position would be perpendicular to the conducting plane or did I iterpret it wrong?

 

[TSny]

Sorry, it was my mistake. I was not orienting the image dipole correctly which led to a sign error on my part. The image dipole is not oriented as shown in your picture (post #5) but as shown in part (a) of the solution of your last post. The expressions for E and N given in the solution look correct. And the direction of the torque is such as to make the equilibrium orientation of the dipole perpendicular to the conducting plane:

equilibrium is $\uparrow$ if initially $-\pi/2 < \theta < \pi/2$
equilibrium is $\downarrow$ if initially $\pi/2 < \theta < 3\pi/2$

where $\theta$ is as shown in the figure for part (a) solution.

Hope I didn't cause you too much of a headache.

 

[Pushoam]

I was not orienting the image dipole correctly which led to a sign error on my part. The image dipole is not oriented as shown in your picture (post #5) but as shown in part (a) of the solution of your last post.

The image dipole given in the book's solution is not -p. I was taking -p as image dipole so that the potential due to p at the plane will get canceled by potential due to -p and hence we will get the potential on the space containing the plane to be 0.
What is wrong with this argument?

 

[TSny]

In your diagram, the image dipole looks to me to be parallel to the real dipole. But they are not parallel (in general). See the figure in the solution part (a).