Torque on a rectangular coil in a uniform magnetic field

[Bolter]

Homework Statement

See image below

Relevant Equations

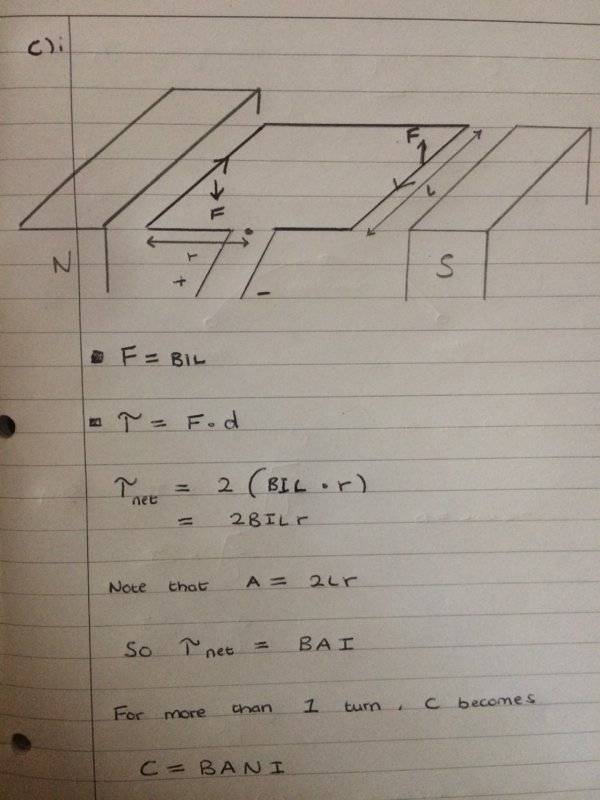
F = BIL

So this was a section taken out from a question which I am trying to do shown below

I have drawn a sketch to help me visualise of what is going on

I have used Fleming's left hand rule to help me determine what direction the force is facing on each side of the coil.

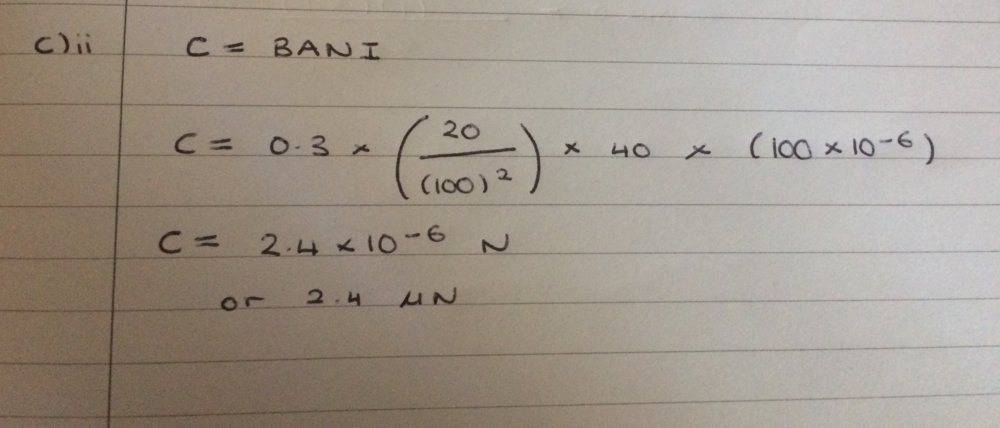
For the last part in c)ii , this is what I would say as the coil rotates:

As the coil rotates from a sideway to a vertical orientation, less magnetic field lines pass through the coil thus torque value decreases to zero. Maximum torque only occurs when the magnetic field is perpendicular to the normal line of the coil. Where as it is a minimum (zero) torque when the magnetic field is parallel to the normal line of the coil

Would that be sufficient to what the question asks for?

Any help would be really grateful! Thanks

 

[kuruman]

The coil has 4 sides. You should explain why you consider only 2 sides in your calculation and ignore the other 2. Also, the uniform magnetic field points left to right as deduced by your pole labels. The coil is not drawn "with its sides perpendicular to the magnetic field lines" because only two sides are drawn perpendicular. The ones you ignored are drawn parallel to the field lines.

 

[Bolter]

The coil has 4 sides. You should explain why you consider only 2 sides in your calculation and ignore the other 2. Also, the uniform magnetic field points left to right as deduced by your pole labels. The coil is not drawn "with its sides perpendicular to the magnetic field lines" because only two sides are drawn perpendicular. The ones you ignored are drawn parallel to the field lines.

For the other 2 sides that I have ignored, I cannot use either Fleming's left hand rule or right hand rule because the direction of current and magnetic field are parallel to each other?

However I believe that no torque is produced on those 2 sides as torque is known to be:

C = BANI sin(theta)

If they are both parallel to the field, then the angle theta is 0 degrees hence sin(0) = 0. Which means C = BANI sin(0) = 0 so zero torque on both those 2 sides?

where angle theta is the angle between the perpendicular of the loop and field line

 

[kuruman]

For the other 2 sides that I have ignored, I cannot use either Fleming's left hand rule or right hand rule because the direction of current and magnetic field are parallel to each other?

As I posted earlier, the problem specifies that "the coil is placed with its sides perpendicular to the magnetic field lines". No current is parallel to the field lines. You need a new drawing.

However I believe that no torque is produced on those 2 sides as torque is known to be:

C = BANI sin(theta)

The torque is not "known" to be that. You are supposed to show that in part (i).

 

[Bolter]

As I posted earlier, the problem specifies that "the coil is placed with its sides perpendicular to the magnetic field lines". No current is parallel to the field lines. You need a new drawing.

The torque is not "known" to be that. You are supposed to show that in part (i).

I have made a new drawing but I can't seem to wrap my head around about what direction the force is acting upon the other 2 sides?

The arrow labelled 'B' on top is indicating the direction of the magnetic field from north to south

Like on one side the direction of current is anti-parallel to the direction of the magnetic field so there should be no force

And on the other side, current is in the direction of the magnetic field but again there would be no force as there's no angle between current or magnetic field?

I'm just very confused right now

 

[Bolter]

The coil has 4 sides. You should explain why you consider only 2 sides in your calculation and ignore the other 2. Also, the uniform magnetic field points left to right as deduced by your pole labels. The coil is not drawn "with its sides perpendicular to the magnetic field lines" because only two sides are drawn perpendicular. The ones you ignored are drawn parallel to the field lines.

Ok maybe my original set up was looking a little wrong here but I have tried making a more simplified correct drawing

Used Fleming's right hand rule on all sides of the coil to determine the direction of force acting on that side

I realized that the top and bottom force are antiparallel with each other so will can cancel out and have no effect on the motion of the coil. But this will also do the same the left and right sides of the coil so the coil wouldn't be rotating at all? It seems like the coil would just stay stationary and has a force stretching it outwards on its sides

 

[kuruman]

For the directions of the field and current you show, the forces must be in the opposite directions. Regardless of that, your conclusion that the torque is zero is correct. My point is that you cannot satisfy the given condition that "the coil is placed with its sides perpendicular to the magnetic field lines" and have non-zero torque. It's an inconsistently-phrased question. If you relax the given condition and rotate the coil by 90^o as you originally had, then the torque is not zero and you have correctly found the expression for it.

 

[Bolter]

For the directions of the field and current you show, the forces must be in the opposite directions. Regardless of that, your conclusion that the torque is zero is correct. My point is that you cannot satisfy the given condition that "the coil is placed with its sides perpendicular to the magnetic field lines" and have non-zero torque. It's an inconsistently-phrased question. If you relax the given condition and rotate the coil by 90^o as you originally had, then the torque is not zero and you have correctly found the expression for it.

Thank you this clears my doubt now. I now understand what you had meant earlier which I had failed to understand before