How Do You Calculate Torque in a Current Loop with a Hanging Mass?

Click For Summary
SUMMARY

The calculation of torque in a current loop with a hanging mass involves the formula Torque = NIABsin(θ), where N is the number of turns, I is the current, A is the area of the loop, B is the magnetic field strength, and θ is the angle between the magnetic field and the normal to the loop. In this scenario, a 10-turn loop carrying a 2.0 A current and a 50 g mass is analyzed. The area A is calculated as 0.1 m * 0.05 m, resulting in A = 0.005 m². The torque is influenced by the orientation of the loop relative to the magnetic field, specifically the value of sin(θ), which is 1 when the loop is perpendicular to the field.

PREREQUISITES
  • Understanding of electromagnetic principles, specifically torque in magnetic fields.
  • Familiarity with the formula Torque = NIABsin(θ).
  • Basic knowledge of current loops and their properties.
  • Ability to calculate area from dimensions of a rectangular loop.
NEXT STEPS
  • Research the effects of varying the angle θ on torque calculations in magnetic fields.
  • Study the implications of multiple turns in a current loop on torque using the formula Torque = NIABsin(θ).
  • Explore the relationship between magnetic field strength (B) and torque in different configurations of current loops.
  • Learn about the physical significance of torque in electromagnetic applications, such as electric motors.
USEFUL FOR

This discussion is beneficial for physics students, educators, and anyone involved in electromagnetism, particularly those studying torque in current loops and magnetic fields.

dtesselstrom
Messages
29
Reaction score
0

Homework Statement


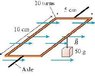
The 10-turn loop of wire shown in the figurelies in a horizontal plane, parallel to a uniform horizontal magnetic field, and carries a 2.0 A current. The loop is free to rotate about a nonmagnetic axle through the center. A 50 g mass hangs from one edge of the loop.


Homework Equations


Torque = u * B
Torque = (I*A) B


The Attempt at a Solution


Ive tried all sorts of things I konw that I is 2.0 A and A is .1 * .05 so that gives .01 * B = Torque and I've set torque equal to just the F of the weight times the radius and diameter and I've also tried doubling the F because the force down on both sides. No matter what I've tried it doesn't seem to work. Answers that I have gotten are 1.225. 2.45, 4.9, and .6125 so if you try this problem and get those they are wrong. Thanks for the help.
 

Attachments

  • knight_Figure_32_80.jpg
    knight_Figure_32_80.jpg
    12 KB · Views: 610
Physics news on Phys.org
If there are 10 turns in the loop, wouldn't you use the equation that incorporates the # of turns?

As far as I know, the 2nd equation you stated holds true for rectangular loops (I can't see your attachment so I don't really know what the problem set up is).

Additionally, if the loops is parallel to the magnetic field...what would sin(theta) be?
 
Last edited:
I can't find any equations in my book for turns in the loop so if you could help me out with that Id appriciated it and I was wondering that myself as for the picture it is set up as a rectangular loop so I wasn't sure that the turns ment anything and wouldn't it make the sin of theta 90 degrees?
 
For any other loop that is not a rectangle, torque=NIABsin(theta), where N=# of turns.
 
ok got it thanks for the help.
 
dtesselstrom said:
ok got it thanks for the help.[/QUO
What is the answer for this question for the existing numbers? Can you help?
 
Did anybody come up with an answer for this question?
 

Similar threads

Torque on current carrying loop/Diploe moment of loop
  • · Replies 3 ·
Replies
3
Views
2K
How Do You Calculate the Magnetic Moment and Torque of a Rectangular Loop?
  • · Replies 3 ·
Replies
3
Views
4K
How Does Torque Relate to Magnetic Dipole Moment in Physics?
  • · Replies 3 ·
Replies
3
Views
4K
Torque on cylinder due to current in loop
  • · Replies 1 ·
Replies
1
Views
3K
How to find the Braking Torque of an Eddy Current Braking Setup?
  • · Replies 26 ·
Replies
26
Views
6K
How does the number of turns in a loop affect the torque in a magnetic field?
  • · Replies 3 ·
Replies
3
Views
12K
Induced current and torque in a rectangular metal loop
  • · Replies 1 ·
Replies
1
Views
2K
Question: How do I account for the wire below the loop when finding net torque?
  • · Replies 1 ·
Replies
1
Views
3K
Solve Torque & Magnetism: Find Magnetic Field Strength
  • · Replies 2 ·
Replies
2
Views
16K
How Is Torque Calculated on a Current Loop in a Magnetic Field?
  • · Replies 1 ·
Replies
1
Views
3K