SUMMARY
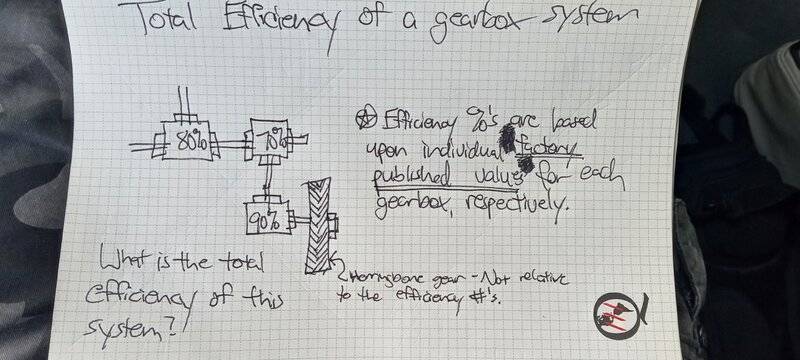
The overall efficiency of a system of gearboxes is determined by multiplying the efficiencies of each individual gearbox rather than averaging them. For example, three gearboxes with efficiencies of 70%, 80%, and 90% yield an overall efficiency of 0.7 x 0.8 x 0.9 = 0.504 or 50.4%. In a scenario with 16 gearboxes, each at 90% efficiency, the actual efficiency drops to approximately 18.5% due to cumulative losses. The type of gearbox—planetary, worm, or helical—affects efficiency, with planetary gears generally offering better performance due to their ability to cancel side forces.
PREREQUISITES
- Understanding of gearbox types: planetary, worm, and helical
- Basic knowledge of mechanical efficiency calculations
- Familiarity with Free Body Diagrams (FBD) in mechanical systems
- Awareness of the impact of bearings on gearbox performance
NEXT STEPS
- Research the efficiency characteristics of different gearbox types
- Learn how to perform Free Body Diagrams (FBD) for mechanical systems
- Study the effects of bearing design on gearbox efficiency
- Explore advanced gearbox configurations and their efficiency implications
USEFUL FOR
Mechanical engineers, automotive engineers, and anyone involved in the design and optimization of gearbox systems will benefit from this discussion.