Tracking travel between orbits in a whirlpool

[StealthyRobot404]

TL;DR Summary: What started as a neat idea for an RPG setting has become more intricate than expected. In a massive whirlpool there are several "orbiting" islands, and I would like an easier way to track sailing time between them.

I was so naive. A giant whirlpool with a bunch of islands that float along was such a simple idea! My desire for meticulous detail has driven me to new lengths, so here I am. I have quite a bit of data already, and an animated tracker for the islands and their orbits.

So, first off, the whirlpool itself is 9,814 miles (15,794 km) in diameter. I'm using a 360 day calendar to make things easier on myself, still with 12 months, 10 days a week. It's divided into temperature zones: Tropic, Temperate, and Arctic. All Islands rotate clockwise with the flow of the water. The current flows at 2.5 mph (4 km/h) [The speed of the current is slightly different in each ring but I'm not sure I want to get into that for this.) The speeds of the islands have been somewhat arbitrarily determined based on density, how much mass is underwater versus how much wind drag it may have based on terrain.

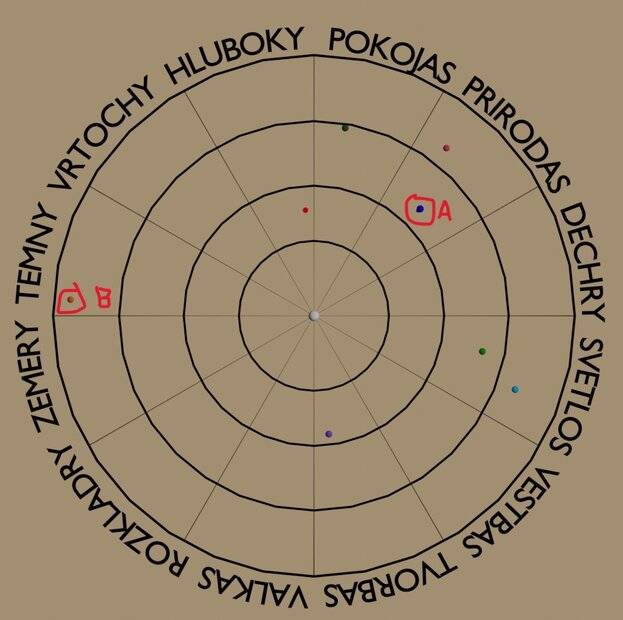
So, Island A has an average distance of 3,024 miles (4,867 km) from the center and a 360 day orbit, giving it an average speed of 2.2 mph (3.5 km/hr).

Island B has an average distance of 4,563 miles (7343 km) from the center and a 840 day orbit, giving it an average speed of 1.4 mph (2.3 km/hr).

Assuming a ship has a speed of 5 mph (8 km/hr), it would take about 95 days for a ship to travel from A to B. The method of doing this is by essentially using a ruler to measure out segments of the travel path, adjusting as needed to find an efficient course.

My big question: Is there an easier way? Some formula that could be devised that accounts for the speed of the islands speeds and locations?

 

[Flyboy]

That’s a really interesting setting. I’m not sure how to calculate that travel time, but I also am willing to just fudge it.

 

[Drakkith]

The current flows at 2.5 mph (4 km/h) [The speed of the current is slightly different in each ring but I'm not sure I want to get into that for this.) The speeds of the islands have been somewhat arbitrarily determined based on density, how much mass is underwater versus how much wind drag it may have based on terrain.

That's a pretty low speed. As long as the above-water portion of the islands are a relatively small fraction of the total then at this speed you won't really have to worry about wind resistance on the islands and you can just assume they all travel at the same speed as the water. You might only need to worry about the speed varying slightly if there are REALLY strong winds for a prolonged period of time or your calculating the positions for them far into the future.

As for travel time between each island, since the water is moving along with the islands, it also carries boats with it. This means that the distance traveled from one island to another within the same ring is just the distance the islands are apart. Imagine you're on an unpowered ship going down a river and you want to send a small motor boat to another unpowered ship that's 200 yards ahead of your ship. Perhaps to trade parts to repair your engines. The motor boat will only travel a distance of 200 yards (relative to the ships) to get from one ship to another, while it might travel 250 yards one way and 150 on the way back according to someone on the shore (or some other value that depends on the river speed). If the motor boat moves at a speed of 100 yards per minute, it will take two minutes each way. Same for your whirlpool scenario, just scaled up.

Things get a bit more complicated as you go from ring to ring. One way to go about this would be:

1. Calculate the time the boat takes to move from its start point to the edge of the next ring.
2. Find how far its destination island has moved during that time.
3. Calculate how long the rest of the journey will take in that new ring to get to the destination island.

This is just a quick and dirty estimate that gets worse as the journey get longer, but it's a starting point at least.