Triangle Problem: Proving DC=AC

[raul_l]

Hi.
What's wrong here?
I'm pretty sure I did all the operations correctly so I must be making some kind of conceptual flaw.

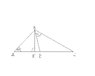
(first see the attachment)

\triangle ABC \sim \triangle BDC
\frac{S_{ABC}}{S_{BDC}}=\frac{AB^2}{BD^2}
\frac{S_{ABC}}{S_{BDC}}=\frac{\frac{AC \times BE}{2}}{\frac{DC \times BE}{2}}=\frac{AC}{DC} \Rightarrow \frac{AC}{DC}=\frac{AB^2}{BD^2}
AB^2=BE^2+AE^2=BC^2-EC^2+(AC-EC)^2=BC^2-EC^2+AC^2-2AC \times EC+EC^2=
=BC^2+AC^2-2AC \times EC
BD^2=BE^2+ED^2=BC^2-EC^2+(EC-DC)^2=BC^2-EC^2+EC^2-2EC \times DC+CD^2=
=BC^2-2EC \times DC+DC^2
\frac{AC}{DC}=\frac{BC^2+AC^2-2AC \times EC}{BC^2-2EC \times DC+DC^2}
\frac{BC^2-2EC \times DC+DC^2}{DC}=\frac{BC^2+AC^2-2AC \times EC}{AC}
\frac{BC^2}{DC}-2EC+DC=\frac{BC^2}{AC}+AC-2EC
\frac{BC^2}{DC}-AC=\frac{BC^2}{AC}-DC
\frac{BC^2-AC \times DC}{DC}=\frac{BC^2-AC \times DC}{AC} \Rightarrow DC=AC

 

[HallsofIvy]

The first thing you are doing wrong is not defining your terms! What is S_ABC? The area of triangle ABC? I am willing to assume that A, B, C are vertices of triangle ABC but what is E? The foot of the altitude on AC? If BE is the length of the altitude of triangle ABC on AC, what right do you have to assert that is also the length of the altitude of triangle BDC on BD?

 

[raul_l]

Erm.. I figured all those things were obvious enough.
So yes, S[abc] is the area of ABC just as S[bdc] is the area of BDC.
E is the foot of the altitude on AC and therefore BE is its length. However, it doesn't say that BE is the length of the altitude on BD. BE is the length of the altitude on DC, because it forms a right angle with the extension of DC (right?). Therefore 1/2xDCxBE is the area of triangle BDC (which can be seen in the 3rd line).
I now it's not much fun to look through these equations but I would really appreciate it if someone could tell me where I have made a mistake. Because otherwise I would be proving that the length of a line segment is equal to the length of it subsegment (not sure whether that's the right word), in this case that the length of AC equals the length of DC.

 

[0rthodontist]

What are you actually trying to do?

 

[raul_l]

What are you actually trying to do?

Good question :)
Sorry I didn't make that clear.
Actually, finding the mistake is the only objective here. A friend of mine showed this to me. He said that he had proven the "theorem" that the length of a line segment is equal to the length of its subsegment (by using a triangle), which was obviously a joke. However, he showed me how he had done that and asked me to find a mistake there. And so far I've got nothing.
If you look at the equations then they're all very simple operations, basically I've only used the Pythagorean theorem and a property of similar triangles. So to answer you question, the objective is to prove this "theorem" wrong.

 

[raul_l]

I just found the answer to this problem.
In the last equation BC^2-AC \times DC=0 and therefore it would be incorrect to assume that DC=AC.

 

[Hubert]

Erm.. I figured all those things were obvious enough.
So yes, S[abc] is the area of ABC just as S[bdc] is the area of BDC.
E is the foot of the altitude on AC and therefore BE is its length. However, it doesn't say that BE is the length of the altitude on BD. BE is the length of the altitude on DC, because it forms a right angle with the extension of DC (right?). Therefore 1/2xDCxBE is the area of triangle BDC (which can be seen in the 3rd line).
I now it's not much fun to look through these equations but I would really appreciate it if someone could tell me where I have made a mistake. Because otherwise I would be proving that the length of a line segment is equal to the length of it subsegment (not sure whether that's the right word), in this case that the length of AC equals the length of DC.

No, (1/2)(DC x BE) does not equal the area of triangle BDC. The height must be a line drawn to the vertex of a triangle.

EDIT: Nevermind. I just proved that I was wrong.