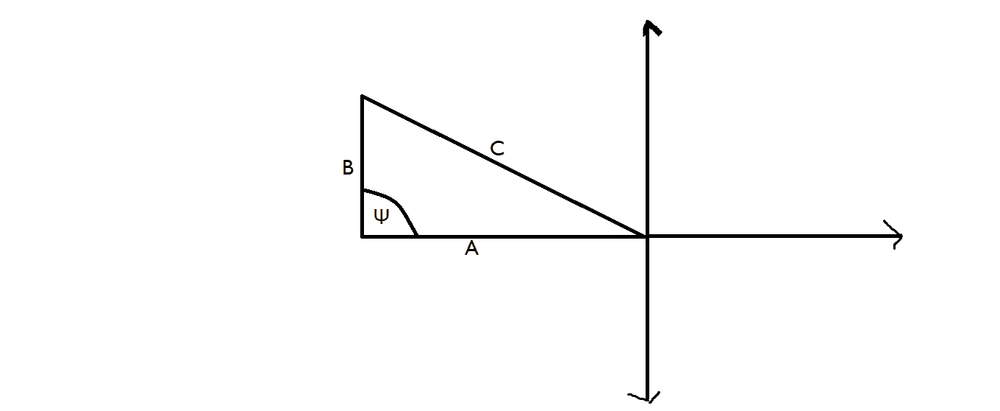
What is the connection between the Law of Cosines and Euclid's teachings?

[SSG-E]

TL;DR Summary

In case of right angled triangles, C^2 = A^2 +B^2 - 2AB cos(Ψ) is shortened to C^2 = A^2 +B^2 because the cosine of the angle "Ψ" which is 90° is equal to 0. But how is its cosine equal to 0.

I

 

[etotheipi]

$\cos{90^{\circ}} = 0$

 

[Adesh]

We can have geometric a proof, but how about this one:
$$
\sin^2 \psi + \cos^2 \psi = 1$$
$$if~\psi = 90^{\circ} ~and~accepting ~\sin 90^{\circ} = 1$$

$$1 +\cos^2 90^{\circ} = 1$$
$$\cos^2 90^{\circ} = 0 $$
$$\cos 90^{\circ}=0
$$

 

[etotheipi]

@Adesh perhaps, but that would rely on knowing $\sin{90^{\circ}} = 1$ and we're back where we started.

There are a few ways of determining the values of trigonometric functions. A useful tool is the so-called unit circle, which consists of a circle of radius 1 centred on the origin in the $x$-$y$ plane. The coordinates of any point on the circle at an angle $t$ to the positive $x$ axis are $(\cos{t}, \sin{t})$, as shown:

If $t = \frac{\pi}{2} = 90^{\circ}$, the point is at the top of the circle. The $x$-coordinate is $0$, and this is the cosine of the angle. It's also useful for determining the signs of trigonometric functions in the different quadrants (I've seen this called the "CAST Diagram" before).

Really you should memorise how $\sin$, $\cos$ and $\tan$ behave at $\theta = 0$, $\theta = \frac{\pi}{6}$, $\theta = \frac{\pi}{4}$, $\theta = \frac{\pi}{3}$ and $\theta = \frac{\pi}{2}$. You can use the unit circle and trigonometric identities to deduce the values for lots more angles from them.

 

[symbolipoint]

But how is its cosine equal to 0.

Not Correct.

 

[symbolipoint]

Summary:: In case of right angled triangles, C^2 = A^2 +B^2 - 2AB cos(Ψ) is shortened to C^2 = A^2 +B^2 because the cosine of the angle "Ψ" which is 90° is equal to 0. But how is its cosine equal to 0.

IView attachment 264987

You can find the proof of Law Of Cosines in some Trigonometry books and some Calculus books. There is an old book by Anton which includes a proof.

 

[mathwonk]

My favorite proofs are propositions 12, 13 Book II, Euclid's Elements.

 

[neilparker62]

Summary:: In case of right angled triangles, C^2 = A^2 +B^2 - 2AB cos(Ψ) is shortened to C^2 = A^2 +B^2 because the cosine of the angle "Ψ" which is 90° is equal to 0. But how is its cosine equal to 0.

cos 90 = sin(90-90) = sin(0) = 0.

Does that now beg the question "how is sin(0) = 0" ?

 

[etotheipi]

cos 90 = sin(90-90) = sin(0) = 0.

Does that now beg the question "how is sin(0) = 0" ?

But you have turned the question into something that is much easier to answer, if you know or can derive the series expansions. Namely...

$\sin{0} = 0 - \frac{1}{3!}0^3 + \frac{1}{5!}0^5 + \dots = 0$

 

[neilparker62]

Proof of Cosine Rule using Ptolemy's Thm

 

[neilparker62]

My favorite proofs are propositions 12, 13 Book II, Euclid's Elements.

 

[etotheipi]

Another way, label the triangle like this:

Pythagoras on the left triangle: $x^2 + h^2 = b^2$
Pythagoras on the right triangle: $a^2 - 2ax + (x^2 + h^2) = c^2$

Now since $b\cos{C} = x$, we finally have $a^2 + b^2 - 2ab\cos{C} = c^2$.

 

[Adesh]

Another way, label the triangle like this:

View attachment 265361

Pythagoras on the left triangle: $x^2 + h^2 = b^2$
Pythagoras on the right triangle: $a^2 - 2ax + (x^2 + h^2) = c^2$

Now since $b\cos{C} = x$, we finally have $a^2 + b^2 - 2ab\cos{C} = c^2$.

Oh you English people! I can see that you have not even used the scale for drawing that perpendicular $h$ and that $h$ is very pointy, it has sharp end points. It’s really an English’s writing (so tough to read).

 

[etotheipi]

Oh you English people! I can see that you have not even used the scale for drawing that perpendicular $h$ and that $h$ is very pointy, it has sharp end points. It’s really an English’s writing (so tough to read).

Yes my hand-writing is terrible, I never got my pen-license in primary school

 

[Leo Liu]

Draw an unit circle and add an additional line on the positive y-axis as the terminal arm. Let z denote the length of the terminal arm, we get: $$\cos(\theta)=\frac x z\implies \cos(90)=\frac 0 1 = 0$$

 

[etotheipi]

Draw an unit circle and add an additional line on the positive y-axis as the terminal arm. Let z denote the length of the terminal arm, we get: $$\cos(x)=\frac x z\implies \cos(90)=\frac 0 1 = 0$$

What do you mean by a terminal arm?

 

[Mark44]

What do you mean by a terminal arm?

I'm pretty sure that he means the ray whose angle is measured relative to the reference direction, the positive x-axis.

 

[robphy]

In some texts, the law of cosines or a polarization identity is used to define the cosine function:
$$\vec C = \vec A +\vec B$$

$\begin{align*} C^2 &= (\vec A+\vec B)\cdot (\vec A+\vec B) =A^2 +B^2 + 2AB\cos\theta \\ \cos\theta_{AB} &\equiv\frac{C^2-A^2-B^2}{2AB} \end{align*}$$\begin{align*} (\vec A+\vec B)\cdot (\vec A+\vec B) &=A^2 +B^2 + 2AB\cos\theta \\ (\vec A-\vec B)\cdot (\vec A-\vec B) &=A^2 +B^2 - 2AB\cos\theta \\ \cos\theta_{AB} &\equiv\frac{(\vec A+\vec B)\cdot (\vec A+\vec B) - (\vec A-\vec B)\cdot (\vec A-\vec B)}{4AB} \end{align*}$

 

[neilparker62]

Another way, label the triangle like this:

Pythagoras on the left triangle: $x^2 + h^2 = b^2$
Pythagoras on the right triangle: $a^2 - 2ax + (x^2 + h^2) = c^2$

Now since $b\cos{C} = x$, we finally have $a^2 + b^2 - 2ab\cos{C} = c^2$.

$h=b\sin\hat{C}$ and $x=b\cos\hat{C}$. Hence:
$$c^2=b^2\sin^2\hat{C}+(a-b\cos\hat{C})^2=a^2 + b^2 - 2ab\cos{\hat{C}}$$, and as a 'bonus': $$\tan\hat{B}=\frac{b\sin\hat{C}}{a-b\cos\hat{C}}$$

 

[Leo Liu]

$h=b\sin\hat{C}$ and $x=b\cos\hat{C}$. Hence:
$$c^2=b^2\sin^2\hat{C}+(a-b\cos\hat{C})^2=a^2 + b^2 - 2ab\cos{\hat{C}}$$, and as a 'bonus': $$\tan\hat{B}=\frac{b\sin\hat{C}}{a-b\cos\hat{C}}$$It

It is a great loss of archaeology that you do not work in that field.

 

[neilparker62]

It is a great loss of archaeology that you do not work in that field.

thanks - cool profile pic by the way. Where is it from ?

 

[Leo Liu]

thanks - cool profile pic by the way. Where is it from ?

View attachment 289504

I found it on a website for sharing wallpapers.

 

[mathwonk]

To me the cosine law became interesting and beatiful only after i learned from euclid, as an old man by then myself, that it is a natural complement to the pythagorean theorem, and can be expressed as areas of rectangles, no formulas needed. It just asks how much excess area does the square on the "hypotenuse" create when the angle opposite is greater than a right angle. And it answers in terms of the area of a simply given rectangle. The side of this rectangle then gives rise to the concept of a cosine. Since it was not taught in my primitive high school geometry course, I did not realize it was a geometry theorem, and only encountered it in a trig course, expressed in mysterious formulas, which did not speak as clearly to me. So it took me almost 50 years to understand this topic, for the simple reason that in the US, geometry is usually not taught from Euclid, as (at least I think) it should be.

Indeed as in post #18, this historical approach does to me fully justify using the deviation in the pythagorean formula, as a definition of the cosine.