Trouble understanding 2-side BH Penrose diagram

[Jimster41]

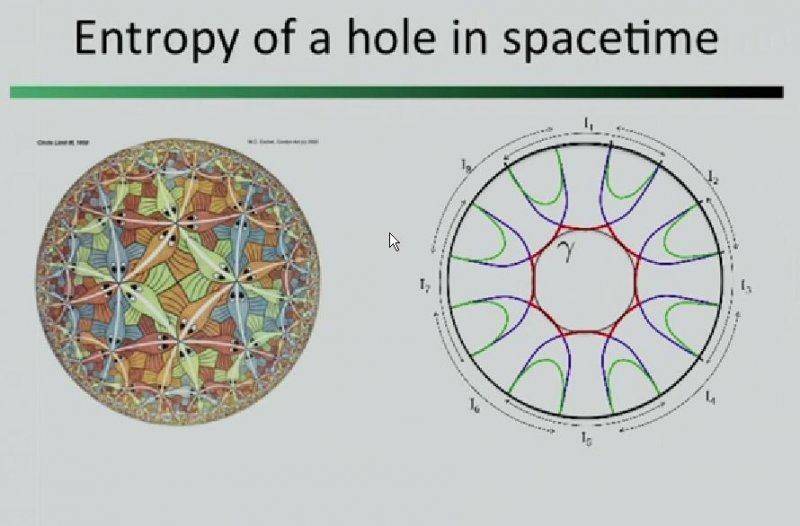
I've seen this a few times now, but it's not quite sinking in? How are the left and right sides of that 2-side BH Penrose diagram disconnected but share the BH? I keep thinking you could go around the black hole.

Trying to think of a metaphor that correctly captures my confusion.
Picturing a literal big BH, with observer A on one side, and observer B say on the opposite side, like two people standing on opposite sides around a fire-pit. Both have flashlights. Both shine their flash lights at the fire, but the light never gets across the fire pit. It just goes into the fire-light, never comes out the other side. They each have no idea the other is there - their locations are disconnected.

But if observer B was standing at 90 degrees from observer B around the firepit, he could shine his light right on A, and vice versus. Those spaces are not disconnected.

So the space that is disconnected from observer A's space is only the space that a light ray would have to "go through the BH" to get to. It is space at a specific angle w/respect to observer A and the BH, aligned more or less opposite observer A from the black hole.

Is that understanding it?The circle in the right-hand diagram being the fire-pit, and the entanglement measure of flashlight shiners A and B being related to their fire-pit circle boundary interval, and the angle of those intervals w/respect to the black hole, or how much of their respective flash-light meets in the BH.

got that from this cool vid by the way from @atyy
which I am trying to follow.

 

[bapowell]

The Penrose diagram of the Schwarzschild black hole shows only 1 spatial dimension -- the radial coordinate. This is possible because the Schwarzschild space is spherically symmetric.

So, for example, a collection of observers circling the black hole at common distance r would be represented by a single point on the Penrose diagram.

 

[stedwards]

I believe he's asking about the Schwarzschild wormhole.

 

[bapowell]

The Kruskal extension of the Schwarzschild black hole that includes the worm hole is also spherically symmetric.

 

[Jimster41]

I get that the Penrose diagram is showing only one spatial dimension. It's just that when I heard Susskind's lecture on it, and then when I saw it in the video linked by @atyy, I got dropped because I was having trouble following the claim that the two sides are "disconnected" spaces, that only connect in the black hole or singularity.

It's clear in the 2d (x=space,y=time) drawing, but in the 3d case (the bound cylinder in the video) the only constraint that seems to make them disconnected, is "geodesic". A non-geodesic would still connect them.

And then this concept of geodesic and arc segment length seems key to the discussion of entanglement entropy around a black hole (in the video), which I have wanted to understand better. I took it to mean that there is something important in terms of entanglement or disentanglement, that has to do with the angular relationship of two respective points around a black hole.

Are two adjacent points around a black hole considered more entangled or less entangled than two points opposite a black hole? I would have said that the one's opposite are more entangled, but I don't quite get why?

 

[bcrowell]

I get that the Penrose diagram is showing only one spatial dimension. It's just that when I heard Susskind's lecture on it, and then when I saw it in the video linked by @atyy, I got dropped because I was having trouble following the claim that the two sides are "disconnected" spaces, that only connect in the black hole or singularity.

It's clear in the 2d (x=space,y=time) drawing, but in the 3d case (the bound cylinder in the video) the only constraint that seems to make them disconnected, is "geodesic". A non-geodesic would still connect them.

A spacelike geodesic could connect them. When we say they're disconnected, we mean that they're causally disconnected. If you have an event A in one of the copies of Minkowski space, and an event B in the other, then A can't lie in B's future light cone, and B can't lie in A's.

And then this concept of geodesic and arc segment length seems key to the discussion of entanglement entropy around a black hole (in the video), which I have wanted to understand better. I took it to mean that there is something important in terms of entanglement or disentanglement, that has to do with the angular relationship of two respective points around a black hole.

Are two adjacent points around a black hole considered more entangled or less entangled than two points opposite a black hole? I would have said that the one's opposite are more entangled, but I don't quite get why?

You seem to be talking about two completely different subjects here. The part about the Penrose diagram is classical. Entanglement is quantum-mechanical.

 

[Jimster41]

Not too surprisingly, my use of the term geodesic was imprecise. I'm confused when you say "copies of Minkowski space". I keep thinking that two observers on opposite sides of a black hole, are in the same space, or at least universe. And they are causally connectable since observer A could go around and give observer B a kick.

I'd be the first to say I'm confused, and intrigued, about the relationship between black holes and quantum mechanics, but I got that two side Black hole Penrose diagram and entanglement right from Susskind. I mean, I have wild cartons about what he's talking about and why, but...

 

[bcrowell]

I'm confused when you say "copies of Minkowski space". I keep thinking that two observers on opposite sides of a black hole, are in the same space, or at least universe. And they are causally connectable since observer A could go around and give observer B a kick.

There's a detailed discussion of this in Seahra, "An introduction to black holes," http://www.math.unb.ca/~seahra/resources/notes/black_holes.pdf , starting at p. 27. Every point on a Penrose diagram represents a 2-sphere. Let's number the regions as in Seahra's fig. 5 on p. 23. Then any point in region I actually represents an entire 2-sphere surrounding the black hole. An event A one side of the black hole and an event B on the opposite side would both be represented by the same point in region I. A point in region IV represents a completely different two-sphere surrounding the black hole.

 

[PeterDonis]

A point in region IV represents a completely different two-sphere surrounding the black hole.

More precisely, a point in region IV represents a 2-sphere surrounding a different horizon for the black hole than a point in region I. In other words, the single black hole region of the spacetime has two horizons, not one. Each of the horizons is surrounded by a different exterior region that goes all the way to a different spatial infinity. Region I is one of those exterior regions; region IV is the other.

 

[Jimster41]

More precisely, a point in region IV represents a 2-sphere surrounding a different horizon for the black hole than a point in region I. In other words, the single black hole region of the spacetime has two horizons, not one. Each of the horizons is surrounded by a different exterior region that goes all the way to a different spatial infinity. Region I is one of those exterior regions; region IV is the other.

Hmm. I was definitely seeing that diagram wrong. Working on the Seahra reference, which is so far helpful.

The location of the other horizon is where? What determines it's location w/respect to the first (if it can be explained at all intuitively, before month it will take for me to get through that primer)?

 

[PeterDonis]

The location of the other horizon is where?

Where it's shown on the diagram.

As far as an observer in Region I is concerned, the other horizon is unreachable (he would have to travel faster than light to reach it). So "where" it is isn't really a meaningful question for the observer in Region I. Similarly, to an observer in Region IV, the horizon between Region I and the black hole is unreachable.

 

[bcrowell]

As far as an observer in Region I is concerned, the other horizon is unreachable (he would have to travel faster than light to reach it). So "where" it is isn't really a meaningful question for the observer in Region I. Similarly, to an observer in Region IV, the horizon between Region I and the black hole is unreachable.

But this does bring up the following, which I'd never thought about and don't think I understand. An observer in region II has both event horizons in her past light cone and therefore can observe both of them. What is the geometry she sees?

 

[PeterDonis]

An observer in region II has both event horizons in her past light cone and therefore can observe both of them. What is the geometry she sees?

Good question. The best way I can think of to work this out is to start with the observation that, in region II, the clear distinction between "outgoing" and "ingoing" radial null geodesics goes away.

In other words, in region I, on any 2-sphere, one can clearly distinguish between incoming light rays from "outside" and incoming light rays from "inside" the 2-sphere. (The former are "ingoing" null geodesics and the latter are "outgoing" null geodesics.) However, once you fall through the horizon into region II, light rays coming from what you used to call "outside" the 2-sphere you are currently on are coming from region I, but light rays coming from what you used to call "inside" that 2-sphere are coming from region IV (as opposed to coming from the "white hole" when you were in region I). In other words, what you used to call the "ingoing" direction, pointing towards the black hole, now looks to you like an "outgoing" direction, pointing towards a different exterior universe (since that's where the light you see coming from that direction is now coming from).

So I think the apparent spatial geometry an observer in region II would see is very strange; looking "outward" (i.e., in the direction that was "outgoing" when they were in region I) they would see one infinite universe, and looking "inward" (i.e., in the direction that was "ingoing" when they were in region I) they would see a different infinite universe.

 

[bcrowell]

So I think the apparent spatial geometry an observer in region II would see is very strange; looking "outward" (i.e., in the direction that was "outgoing" when they were in region I) they would see one infinite universe, and looking "inward" (i.e., in the direction that was "ingoing" when they were in region I) they would see a different infinite universe.

Hmm...this doesn't quite make sense to me, or maybe I'm not understanding. Suppose that Alice infalls from region I, and Bob infalls from region IV. They rendezvous and have a tea party, and while they're sipping their tea, they look at light from regions I and IV. Do they see the sky split into two hemispheres?

 

[PeterDonis]

Suppose that Alice infalls from region I, and Bob infalls from region IV. They rendezvous and have a tea party, and while they're sipping their tea, they look at light from regions I and IV. Do they see the sky split into two hemispheres?

Not exactly; it's weirder than that. Alice will say that the direction she came from is "outgoing", while the direction Bob came from is "ingoing"; Bob will say the reverse. These are radial directions, so it's as if they are meeting on the surface of a transparent "planet", and each one points in the direction they came from, and to Alice, she is pointing "up" while Bob is pointing "down", but to Bob, he is pointing "up" while Alice is pointing "down". So to each one, the universe the other one came from looks "inside out"--the direction "towards infinity" in that universe looks like the direction "towards the center" of their universe.

 

[stedwards]

Not exactly; it's weirder than that. Alice will say that the direction she came from is "outgoing", while the direction Bob came from is "ingoing"; Bob will say the reverse.

Does this mean that while Bob is sipping tea, Alice is regurgitating hers?

 

[Jimster41]

There's a detailed discussion of this in Seahra, "An introduction to black holes," http://www.math.unb.ca/~seahra/resources/notes/black_holes.pdf , starting at p. 27. Every point on a Penrose diagram represents a 2-sphere. Let's number the regions as in Seahra's fig. 5 on p. 23. Then any point in region I actually represents an entire 2-sphere surrounding the black hole. An event A one side of the black hole and an event B on the opposite side would both be represented by the same point in region I. A point in region IV represents a completely different two-sphere surrounding the black hole.

In the Susskind lecture I saw, it was all about Bob and Alice's tea party BTW, and whether or not they could have entanglement across two different horizons while sipping.

I'm really enjoying that paper. However I'm still trying to see where it is made clear, and by what cause, an "outgoing null geodesic" from region I must reach "time-like" +infinity before entering region IV from the direction of negative time-like Infinity. I've been going back and forth trying to find where I missed it.

One thing am just downright confused about) On page 11 he says (about Fig 2) "it is hard not to notice that the null trajectories all approach the $r=2M$ surface in the limit of $t\rightarrow \pm \infty$. In fact, the limiting case of both families of ingoing and outgoing rays seems to be $r=2M$.
I can see this if you are "backing down" outgoing ray, but if you are "outgoing" you aren't going to wind up and $r=2M$ that I can see? So I must just be over-thinking that one. He must just be talking about how the end-point of incoming and the starting point of outgoing converge to the Killing H.

More to the point of my confusion, If there are two spherically symmetric horizons, located in our universe, say in a space the size of our solar system, an observer at some location on/near Horizon 1 (therefore in region I) should be able to shine a light ray toward horizon 2 right? It would arrive there in at the other Horizon (in region IV) from past infinity?

This does seem problematic because the light would have had to head off in two directions at once, one of which is "outgoing" from region I, the other of which is "incoming" to the same singularity?

This sounds kindof like Alice's tea she is re-drink-itating.

 

[PeterDonis]

Does this mean that while Bob is sipping tea, Alice is regurgitating hers?

No. Both of their proper times go "in the same direction"--or, to put it another way, both of them agree on which half of their light cone, at the event where they meet, is the "future" half.

 

[PeterDonis]

I'm still trying to see where it is made clear, and by what cause, an "outgoing null geodesic" from region I must reach "time-like" +infinity before entering region IV from the direction of negative time-like Infinity

This is not something that's included in the maximally extended Schwarzschild spacetime, i.e., it's not included in the idealized model we have been discussing. It's something extra that gets added on. I haven't looked in detail at the math behind the add-on, but personally, I don't see how the add-on is meaningful physically, since the idealized spacetime with region IV in it does not describe an actual black hole formed by collapse of a massive object like a star. The spacetime describing a realistic black hole formed by collapse contains only region I (the original exterior region), region II (the black hole), and a non-vacuum region containing the matter that collapses. See, for example, here:

http://backreaction.blogspot.com/2009/11/causal-diagram-of-black-hole.html

 

[bcrowell]

Not exactly; it's weirder than that. Alice will say that the direction she came from is "outgoing", while the direction Bob came from is "ingoing"; Bob will say the reverse. These are radial directions, so it's as if they are meeting on the surface of a transparent "planet", and each one points in the direction they came from, and to Alice, she is pointing "up" while Bob is pointing "down", but to Bob, he is pointing "up" while Alice is pointing "down". So to each one, the universe the other one came from looks "inside out"--the direction "towards infinity" in that universe looks like the direction "towards the center" of their universe.

It sounds to me like you're describing something indistinguishable from what I suggested, which was that their sky was split into hemispheres. When you describe Alice pointing "up" according to her, it sounds like you're describing her pointing into 2pi worth of solid angle that she calls up. From the surface of a transparent planet, you don't see a sphere; you see two hemispheres.

 

[PeterDonis]

When you describe Alice pointing "up" according to her, it sounds like you're describing her pointing into 2pi worth of solid angle that she calls up

That's not what I'm trying to describe. Let me drop a spatial dimension to make it clearer.

Suppose Alice and Bob are 2-dimensional creatures who start at opposite ends of a very long surface that is shaped like two funnels connected at their narrow parts (note that the surface is their "universe", or more precisely a spacelike slice of their universe at an instant of time--a circle going around the surface corresponds to a 2-sphere in our 3-dimensional space). They both travel towards each other and meet on the circle at which the two funnels are connected. Each one points in the direction they came from and calls that direction "up". They are pointing in opposite directions, but those directions do not divide the circle they are on into two half-circles; both of them say that their "sky" consists of a whole circle. They only disagree on which direction along the surface, i.e., orthogonal to the circle, is "up". Each one, looking in the direction the other is pointing, thinks of that direction as "down", but instead of a "center" being there (i.e., a point at which the "funnel" they are on narrows down to a point, so it's a cone instead of a funnel), a whole other universe is there (i.e., a second funnel expanding outward to larger and larger circles).

Adding back the extra spatial dimension, we have Alice and Bob both arriving at the same 2-sphere from opposite directions, and each one pointing back in the direction they came from and calling it "up". But each one's "up" occupies the entire sky--all 4 pi worth of solid angle. When each one looks in the direction they were calling "down" (i.e., anywhere in the whole 4 pi of solid angle, but in the opposite direction to the one they were calling "up"), instead of seeing 2-spheres of decreasing radius, down to a point at the "center", they see a second set of 2-spheres of increasing radius, out to a second spatial infinity.

Perhaps it might help to consider, instead of just one Alice and Bob, a whole family of A observers and B observers, each family taking up an entire 2-sphere, i.e., an entire 4 pi worth of solid angle. Each family starts out far out in their exterior region and falls together; they can measure that they are getting closer together, so the 2-sphere that they occupy is decreasing in radius. Each family falls through the horizon bounding its exterior region, and then, once inside the black hole, they meet. Each member of each family will meet up with a corresponding member of the other family, and each corresponding A-B pair will find their "up" directions being opposite, even though both families occupy all 4 pi worth of solid angle; and if each member of each A-B pair looks in their "down" direction, they will see a second universe there.

The really weird part is that, even after the two families meet up, they will continue to fall through 2-spheres of decreasing radius; i.e., they can see the second universe in the direction they were calling "down", but they can't reach it, because what they see is in their past light cone, but what they can reach is in their future light cone.

 

[PeterDonis]

Btw, another issue that should be mentioned is that, inside the black hole region, the concept of "space" as something fixed that objects can "move through" does not work. Spacetime inside the black hole is not static; all future-directed timelike and null curves must have continually decreasing radial coordinate $r$, until they hit the singularity. That's the reason that Alice and Bob can never reach the second exterior universes that they can see in their "down" direction. Basically, the direction they are seeing as "down" is no longer the same as the direction they are actually falling.

 

[bcrowell]

Suppose Alice and Bob are 2-dimensional creatures who start at opposite ends of a very long surface that is shaped like two funnels connected at their narrow parts (note that the surface is their "universe", or more precisely a spacelike slice of their universe at an instant of time--a circle going around the surface corresponds to a 2-sphere in our 3-dimensional space). They both travel towards each other and meet on the circle at which the two funnels are connected. Each one points in the direction they came from and calls that direction "up". They are pointing in opposite directions, but those directions do not divide the circle they are on into two half-circles; both of them say that their "sky" consists of a whole circle. They only disagree on which direction along the surface, i.e., orthogonal to the circle, is "up". Each one, looking in the direction the other is pointing, thinks of that direction as "down", but instead of a "center" being there (i.e., a point at which the "funnel" they are on narrows down to a point, so it's a cone instead of a funnel), a whole other universe is there (i.e., a second funnel expanding outward to larger and larger circles).

Sorry, but although your description is very clear, I'm still reaching the opposite conclusion.

Let's define two circles.

Circle C1 goes around the throat like a necklace. It's the "circle at which the two funnels are connected" in your description. It's not contractible. Their position P is a point on C1.

Circle C2 is a circle centered on P, confined to a neighborhood of P. It's contractible to P.

You seem to be saying that C1 is their sky. I don't think that's right. C2 is their sky, which is split into two half-circles.

I could be wrong, but I think you're incorrectly mixing up global and local notions. Locally space is Minkowski, so their perception of their sky has to be something that can be describable in Minkowski space. Your C1 is global in the sense that it can't be contracted to P, so it can't correspond to their sky.

Think of it in terms of using your outstretched arm to point to a direction in the sky. Your arm forms a spacelike vector whose tip lies on C2. The vector is formed by taking a null vector from your past light cone, projecting out the part orthogonal to your own world-line, and normalizing it to the length of your arm. The fact that your arm is short corresponds to the idea that C1 is confined to a neighborhood of P and contractible to P.

 

[PeterDonis]

You seem to be saying that C1 is their sky. I don't think that's right. C2 is their sky, which is split into two half-circles.

Actually, it's sort of both of these, and sort of not quite either of these.

The "sky" I'm referring to is really the past light cone of the entire family of Alices (or Bobs)--in the funnel analogy, there is a family of Alices coming in from the right, all arranged around a circle of gradually decreasing circumference, and a family of Bobs coming in from the left, all arranged around a circle of gradually decreasing circumference. The past light cone of the family of Alices has two portions, the "up" portion (coming in from infinity), and the "down" portion (coming in from the white hole region until they cross the horizon, then coming from the second exterior region). Each of these portions, for the whole family of Alices, occupies $2 \pi$ worth of circle circumference, or $4 \pi$ worth of solid angle in the full 4-d spacetime case.

Here's another way to look at it. Suppose we are in flat spacetime, and we just have one circle's worth of Alices, all falling in from infinity and meeting at the "center" at a point. At any given instant before all the Alices meet, the past light cone of the whole set of Alices has two portions: an "up" portion (coming in from infinity) and a "down" portion (coming out from the center). Now in this case (and maybe this is where the disconnect is), the "up" portion and the "down" portion both occupy a full $2 ]\pi$ of circle circumference (or $4 \pi$ of solid angle in the 4-d spacetime case), but the two portions are fundamentally different because one is coming from "all over the sky" (for example, if you were standing on a transparent Earth, you could see starlight from the part of the sky opposite to you coming through the Earth and reaching you), while the other is only coming from a finite region of space, the part "inside" your radius (since it's coming from the center), so it will not appear to be coming from "all over the sky".

If we now go to the black hole case, however, and the family of Alices has fallen through the horizon, the above distinction between the two portions of the past light cone is no longer there: the "down" portion (the part that, in the flat spacetime case, was coming from the center) is now coming from a spatially infinite region, just like the "up" portion. So light from both exterior regions will now (I think) appear to be coming from "all over the sky". I wasn't clear about that in prior posts. (Note also that this happens as soon as the Alices or Bobs pass through their respective horizons; it is not something that just happens suddenly when they meet.)