Elnur Hajiyev
- 40
- 0
According to Cosmic Sensorship Conjecture, naked singularities are prohibited in General Relativity. To my knowledge, naked singularity means light from the singularity can escape to infinity.
In Reissner-Nordström metric, references say naked singularity appears only if ##GM^2<P^2+Q^2##. However in ##GM^2>P^2+Q^2## case, according to the Penrose diagram below, light from the singularity which is a timelike surface can take a path which leads to the New Universe.
Does it mean, an observer can see the singularity while he/she is in the wormhole, white hole and in the new universe? Isn't it considered as a naked singularity?
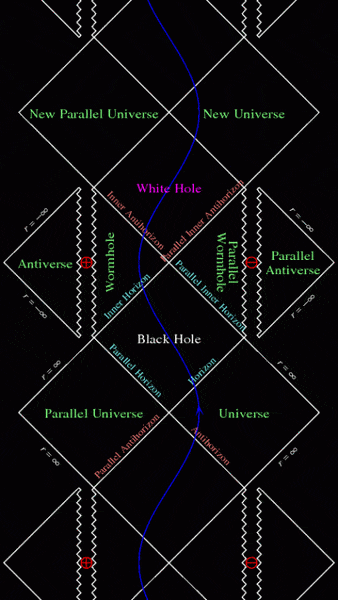
In Reissner-Nordström metric, references say naked singularity appears only if ##GM^2<P^2+Q^2##. However in ##GM^2>P^2+Q^2## case, according to the Penrose diagram below, light from the singularity which is a timelike surface can take a path which leads to the New Universe.
Does it mean, an observer can see the singularity while he/she is in the wormhole, white hole and in the new universe? Isn't it considered as a naked singularity?