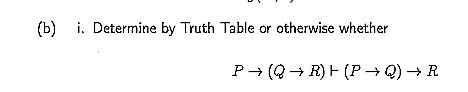Truth Table Precedence: Evaluating Implication Rules

[lyd123]

Hello!
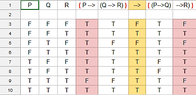
The question is attached.

I know that " $\implies $ " (implies) has precedence from right to left. But because " l- " appears after
P$\implies ($Q $\implies$ R ), in my truth table do I evaluate:(P$\implies ($Q $\implies$ R ) ) $\implies$ ((P$\implies$Q ) $\implies$ R ) )
or

P$\implies ($Q $\implies$ R ) $\implies$ (P$\implies$Q ) $\implies$ R )

Thank you for any help. :)

 

[Evgeny.Makarov]

The turnstile separates formulas but is not a logical connective itself. Therefore $$A\vdash B$$ is equivalent to the fact that $$A\to B$$ is a tautology. This formula has $A$ and $B$ as subformulas joined by $\to$, but it cannot have a subformula that consists of a strict subformula of $A$ and $B$, for example. So it's wrong to consider $P\to(Q\to R)\to(P\to Q)\to R$, which is $P\to((Q\to R)\to((P\to Q)\to R))$ because it has a subformula $(Q\to R)\to((P\to Q)\to R)$, which consists of a part of $A$ and the whole $B$.

I know that " $\implies $ " (implies) has precedence from right to left.

I also like this convention, but I've seen textbooks that consider $\to$ to be left-associative, so one has to be careful.

 

[lyd123]

I think I understand now.. so I should use (P⟹(Q ⟹ R ) ) ⟹ ((P⟹Q ) ⟹ R ) ),
which would give me the attached truth table.
View attachment 8719

So it is not a tautology. Is this correct?

 

[Evgeny.Makarov]

Yes, it is correct. The converse implication is a tautology. This follows from the fact that $P\to Q\to R$ is equivalent to $PQ\to R$ (I omitted conjunction) and $PQ$ implies $P\to Q$.

There is a typo in column R, second last row.

 

[topsquark]

Just a quick question from a novice.

Do [math]\implies[/math] and [math]\rightarrow[/math] mean the same thing? I note that the OP and Evgeny.Makarov are using two different symbols.

-Dan

 

[Evgeny.Makarov]

Do [math]\implies[/math] and [math]\rightarrow[/math] mean the same thing? I note that the OP and Evgeny.Makarov are using two different symbols.

This completely depends on the textbook or other source. Implication can be denoted by $\rightarrow$, $\to$ and $\supset$, and in addition arrows can be short of long. Some authors use different notations for metalevel (a contraction for "if... then..." in English) and object level (a part of the formal language we study) implications. I used a single arrow because it occurs in the attached image in post #1, which I assume comes from the instructor, and because it is shorter in LaTeX ([m]\to[/m] vs [m]\Rightarrow[/m] or [m]\Longrightarrow[/m]).