- #1
AwesomeTrains
- 116
- 3
Hello PF,
first of all I don't know where to put this post as it's not exactly a homework question but a clarification question for a project.
I'm going through the derivation of the effective permeability of two stacked medias, given the polarization of an incoming EM wave but I'm stuck at the point shown in the picture.
The title of the paper is "Electromagnetic Properties of a finely Stratified Medium" by S.M. Rytov in 1956 (I can share it if it's needed).
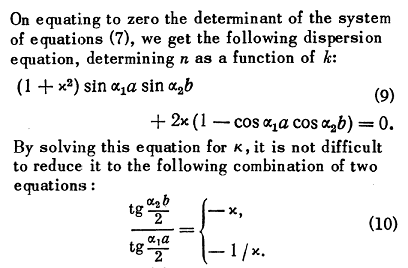
$$\frac{sin(x)}{cos(x)} = tg(x)$$
I don't understand the notation they use and how they solve equation (9).
Does it mean $$\frac{tg\frac{b\alpha_2}{2}}{tg\frac{a\alpha_1}{2}}$$ is equal to [itex] -\chi [/itex] and [itex]-1/\chi[/itex]? Or how is it supposed to be understood?
Regarding how to solve the equation the closest I get is this: $$\frac{1+\chi^2}{2\chi}\ \ tg(a\alpha_1)\ \ tg(b\alpha_2)+(cos(a\alpha_1)\ \ cos(b\alpha_2))^{-1} = 1 $$
first of all I don't know where to put this post as it's not exactly a homework question but a clarification question for a project.
I'm going through the derivation of the effective permeability of two stacked medias, given the polarization of an incoming EM wave but I'm stuck at the point shown in the picture.
The title of the paper is "Electromagnetic Properties of a finely Stratified Medium" by S.M. Rytov in 1956 (I can share it if it's needed).
Homework Statement
Homework Equations
$$\frac{sin(x)}{cos(x)} = tg(x)$$
The Attempt at a Solution
I don't understand the notation they use and how they solve equation (9).
Does it mean $$\frac{tg\frac{b\alpha_2}{2}}{tg\frac{a\alpha_1}{2}}$$ is equal to [itex] -\chi [/itex] and [itex]-1/\chi[/itex]? Or how is it supposed to be understood?

Regarding how to solve the equation the closest I get is this: $$\frac{1+\chi^2}{2\chi}\ \ tg(a\alpha_1)\ \ tg(b\alpha_2)+(cos(a\alpha_1)\ \ cos(b\alpha_2))^{-1} = 1 $$

