Two Beam Problem: Solve 6 Equations, 7 Unknowns

[robot6]

Homework Statement

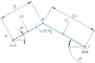
I have a two beam problem, see illustration below. The problem requires a solution for the left beam and for the right beam.

Relevant Equations

$\Sigma F_x = 0$
$\Sigma F_y = 0$
$\Sigma M = 0$

I've drastically simplified the problem for the sake of discussion. The problem is that I end up with six equations and seven unknowns. Let $R_{AX}$ (and similar) be the reaction force at the A node in the rightward direction on the page, and $R_{AY}$ (and similar) be the reaction force at the A node in the upward direction on the page. $M$ is an applied moment and $M_B$ is the reactive moment at node B.

For the left beam, I have:
$R_{AX}+R_{BX}+F_1\sin(\alpha) = 0$
$R_{AY}+R_{BY}-F_1\cos(\alpha) = 0$
$R_{AX}L_1\sin(\alpha)-R_{AY}L_1\cos{\alpha}+M+M_B=0$

For the right beam, I have:
$R_{BX}+R_{CX}-F_2\sin(\alpha)=0$
$R_{BY}+R_{CY}-F_2\cos(\alpha)=0$
$R_{CX}L_2\sin(\alpha)+R_{CY}L_2\cos{\alpha}+M_B=0$

So I have six equations and seven unknowns, namely, $R_{AX}, R_{AY}, R_{BX}, R_{BY}, R_{CX}, R_{CY}, M_B$. What am I missing?

Thank you for your great kindness and answering.

 

[robot6]

The suspense is killing me. Pun intended...

 

[robot6]

Hm. I think that $M_B$ may not exist... because it's accounted for in $R_{A}, R_{B},$ and $R_{C}$.

 

[robot6]

OK I have convinced myself that $M_B$ should be removed. Does it make sense, then, that M should appear in both the third and sixth equations, or should it only appear in one of them?

 

[haruspex]

I am unclear what M and M_B represent in the diagram. Is M an external torque applied only to the left hand beam, while M_B is the torque the beams exert on each other?
If the joint is a hinge, yes, M_B can be dropped as the beams cannot exert torques on each othe.

The signs look inconsistent in your first equation in post #1.

Always make it clear what axis you are using for torque equations. Why do the F forces not appear in those?

 

[robot6]

M is an external torque applied (called a "moment" in this notation, from a different country.)

Sign for equation 1: RAX points to the right, RBX points to the right, and F points to the right, so all should be positive, in my opinion. How is it incorrect?

AH! since they drew M the way I drew it, it looks like M is positive. I-hat (index finger) x j-hat (middle finger) should point out of the paper (thumb). Pointing out of the paper (thumb) means counterclockise (way fingers go). At least that's how my right hand looks... Did I do something wrong?

 

[robot6]

Oh the axis for the torque equation is k-hat.

 

[robot6]

I finally did get a 6x6 matrix with det=29 so I think I solved it. Thanks to Octave!

 

[haruspex]

Sign for equation 1: RAX points to the right, RBX points to the right, and F points to the right, so all should be positive, in my opinion. How is it incorrect?

You are right, the problem is with the fourth and fifth equations. If the right-hand beam exerts a force F_x on the left one then the left exerts a force -F_x on the right.

the axis for the torque equation is k-hat.

Unless an origin is specified, that is only a direction, not an axis. Are you taking B as origin?

 

[robot6]

Yes, B is origin, which makes it simpler because M is about B.

 

[robot6]

By the way it is so helpful that you point out that I need to review equations 4 and 5.

 

[robot6]

I think they are correct, too, because

in equation 4, RBX is positive to the right, RCX is positive to the right, but F2 is pointing towards the left, so it is negative;

in equation 5, RBY is positive up, RCY is positive up, but F2 is pointing down, so it is negative as well.

i am sorry I did not label the R's, but they are all pointing the same direction, + to the right and + up. F's are not pointing in this direction, though.

 

[haruspex]

in equation 4, RBX is positive to the right

That would be fine if you were defining R_BX as a force left beam exerts on right beam, but in equation 1 you defined it as a force right beam exerts on left.
So the force left exerts on right is -R_BX.