Two Connected Masses Swinging on Two Springs - Classic. Mech

[Hunter Bliss]

Homework Statement

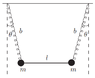
So in this exercise, two masses m connected by a massless rod with length l are swinging from two springs with constant k and length b. The two springs also make an angle Ө with the vertical. This angle, for this exercise specifically, is very small. (Gravity can also be neglected.)

If the movement can only take place in the XY plane and the springs can't be bent (only compressed and stretched), what is the eigen frequency of the system?

Attached is a diagram of the problem.

Homework Equations

I know the relationship between Newton and Hooke's Law will be important, so: F = m·x″ = -k·x

I have a feeling the frequency itself will be solved using differentials and the determinant of the matrix of motion, but those formulas can come later if necessary.

Since the angle Ө is small, it could be useful to remember that: sin(θ)≈θ, cos(θ)≈1

The Attempt at a Solution

I've attached my approach so far, but I'll explain it a little more so you have an idea of what I'm thinking.

Since the masses are connected by a constant distance and the springs can only be stretched and compressed, the swinging motion will be a superposition of the spring forces in the x and y direction. That means the force in each direction can be determined using trig, for example F = -k·x = -k·cosθ·b in the y direction. (In the case of y, y1 = y2 since the masses basically move up and down in the y direction.)

I also thought it might be useful to observe only the center of mass of the two points since that should effectively reduce the problem to one set of coordinates.

Once I started messing around with matrix form and trying some differentials, I lose the intended form. Hopefully someone can help me!

Thanks guys!

 

[Hunter Bliss]

Anybody have an idea?