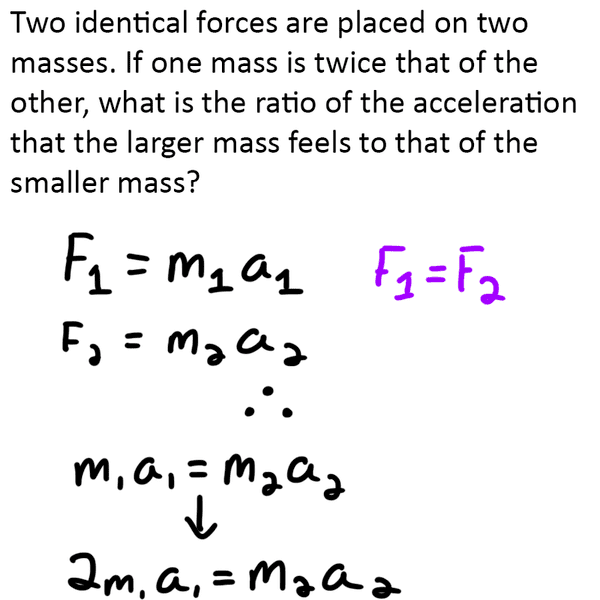Two identical forces on two different masses....

  • Thread starter Thread starter EthanVandals
  • Start date Start date
  • Tags Tags
    Force Forces Mass
Click For Summary
SUMMARY

The discussion centers on the relationship between two masses, m1 and m2, where m1 is twice the mass of m2. The correct equations to analyze their acceleration are established as m1a1 = m2a2 and 2m1a1 = m2a2. The user successfully derives the ratio of their accelerations, concluding that the mass m1 accelerates at half the speed of m2, resulting in a ratio of 2:1. This clarification resolves the initial confusion regarding the equations and ratios presented.

PREREQUISITES
  • Understanding of Newton's Second Law of Motion
  • Familiarity with mass and acceleration concepts
  • Basic algebra for manipulating equations
  • Knowledge of ratios and proportional relationships
NEXT STEPS
  • Study Newton's Second Law of Motion in detail
  • Learn how to derive equations of motion for multiple masses
  • Explore the concept of ratios in physics problems
  • Practice solving problems involving mass and acceleration
USEFUL FOR

Students of physics, educators teaching mechanics, and anyone interested in understanding the dynamics of mass and acceleration relationships.

EthanVandals
Messages
55
Reaction score
2
Member advised to use the homework template for posts in the homework forums.
Here is all the work I have done so far (hopefully it is right). My brain somewhat shuts down when it comes to ratios.
sv5B5Ds.png
 
Physics news on Phys.org
no, that equation is not right. Identify which mass is m1 and which is m2, then one mass is twice the other. Correct your equation accordingly, then solve for the ratio.
 
You wrote:
m1a1 = m2a2
2m1a1 = m2a2

Those two equations contradict each other. Why don't you write an equation for m1 in terms of m2. Then you can substitute for m1 or m2 into the first equation above.

P.S. Welcome to Physics Forums.

Edit: Sorry PhantomJay. I just now saw your post.
 
TomHart said:
You wrote:
m1a1 = m2a2
2m1a1 = m2a2

Those two equations contradict each other. Why don't you write an equation for m1 in terms of m2. Then you can substitute for m1 or m2 into the first equation above.

P.S. Welcome to Physics Forums.

Edit: Sorry PhantomJay. I just now saw your post.
So something more like this then? I got this far, then got confused again as to what kind of ratio I'm supposed to get since I'm not given any values. If I divided by M2, then it would give me (2)A1=A2...so is that saying that the mass that is double the size of the other one is going to accelerate at half the speed of the smaller mass? And would the ratio then be 2:1? Thanks for all your help! :)

EDIT: I'm not sure why my new work isn't showing up...The basics are that I set M1=(2)M2, therefore (2)M2A1=M2A2.

http://imgur.com/a/XdNIG
 
  • Like
Likes   Reactions: TomHart
EthanVandals said:
The basics are that I set M1=(2)M2, therefore (2)M2A1=M2A2.

Edit: Sorry, I read your edit and missed above it. You got the ratio right: 2:1
 

Similar threads

Misunderstanding Work-energy theorem and center of mass properties
  • · Replies 7 ·
Replies
7
Views
2K
Explain why applying different forces to objects of different masses result in different accelerations
  • · Replies 9 ·
Replies
9
Views
2K
Magnitude of buoyant force in fluids of different densities
  • · Replies 17 ·
Replies
17
Views
2K
Two spring-coupled masses in an electric field (one of the masses is charged)
  • · Replies 1 ·
Replies
1
Views
1K
A cylinder connected to a hanging mass
  • · Replies 21 ·
Replies
21
Views
1K
Thermodynamic Work vs Mechanical Work
  • · Replies 3 ·
Replies
3
Views
1K
Force pulling on a string at an angle with a block at the other end
  • · Replies 2 ·
Replies
2
Views
1K
Center of mass and momentum- A question about systems
  • · Replies 25 ·
Replies
25
Views
2K
Struggling to make relation between elastic force and height
  • · Replies 11 ·
Replies
11
Views
915
Olympiad dynamics problem with 3 masses and a pulley
  • · Replies 17 ·
Replies
17
Views
3K