Two Mass Three Rope Tension Problem

[HS21]

Homework Statement

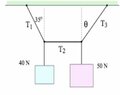
There are two blocks with weights 40N and 50N. The first block is connected to the ceiling at an angle 35 degrees to the left by rope 1 with tension T1 while the second block is connected to the ceiling by rope 3 with tension T3. In between, the first and second block is rope 2 with tension T2. Find T1, T2, T3, and theta. Refer to the attached image.

Relevant Equations

T1=(mg)/[sin(55)]

T2=T1cos(55)

What I did first is to find the tension T1 and T2;

T1=(mg)/[sin(55)]
T1=(40N)/[sin(55)]
T1=48.83N

T2=T1cos(55)
T2=(48.83N)[cos(55)]
T2=28.01N

Now I do not know how to proceed. Can someone help me?

 

[PeroK]

Can you generate two equations involving the unknowns $T_3$ and $\theta$? That would allow you to solve for both unknowns.

 

[Lnewqban]

The magnitude of T2 is the same in both directions.
Vectors T2 and 50N are perpendicular to each other; therefore, the Pythagoras' theorem can be used to determine the magnitude of T3.