Two masses which are connected each other with a spring

[Diff.Ed]

Homework Statement

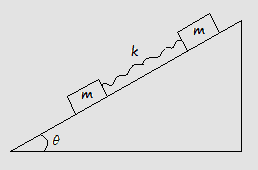
Two blocks both of mass $m$ are placed on an inclined plane making an angle $\theta$ with the ground. The two masses are connected with a spring of spring constant $k$. The coefficient of kinetic friction is $\mu _k$ for both blocks. Assume that the spring is initially stretched to a length $L+x_0$ where $L$ is its equilibrium length when it is at rest on a flat surface. Find the displacement of the two blocks ALONG THE INCLINE as a function of time,t, assuming that at that particular time the spring is still stretched. (Hint : Call the displacement of the leading block along the inclined plane $x_1$. Write the displacement of the trailing block in terms of $x_1$ and stretch in the spring, $x$. You will have two time-dependent equations in two unknowns.)

Related Equations
F=-kx (Hooke's Law), differential equations

The attempt at a solution

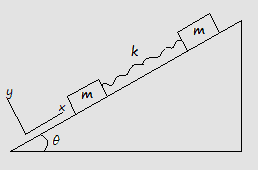
$m\frac{d^2x_1}{dt^2}=-k(x_1+x_0)-mg\sin\theta+\mu _k mg\cos\theta$​

and general solution of this diff. equation

$x_1 = A\sin(\sqrt{k/m}t) + B\cos(\sqrt{k/m}t) - \frac{kx_0+mg\sin\theta+\mu _k mg\cos\theta}{k}$

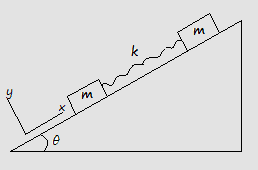
$m\frac{d^2x_2}{dt^2}=k(x_1+x_0)-mg\sin\theta+\mu _k mg\cos\theta$​

I couldn't continue anymore. Could you help me ?

 

[ehild]

Draw the direction of motion of both bodies: The force of friction acts in the opposite direction. Note that the displacement of both bodies influences the length of the spring, so both x1 and x2 influences the spring force.

ehild