Two Parallel Wires: Magnetic Fields

[ShotgunMatador]

Homework Statement

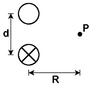
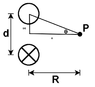
Two long parallel wires are a center-to-center distance of 1.10 cm apart and carry equal anti-parallel currents of 9.70 A. Find the magnitude of the magnetic field at the point P which is equidistant from the wires. (R = 10.00 cm). (See Attachment for orientation)

I = 9.7 A
Distance from current source = √(.1²+(.011/2)²) = 10.015 cm

Homework Equations

B_{infinite wire}= μ_i*I/2*pi*r

The Attempt at a Solution

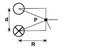
Knowing the upper wire's magnetic field rotates counterclockwise and the lower wire rotates clockwise using RHR 2. So the y components at point P are equal but opposite. So we know the magnitude at Point P is going to be 2 times the x component of the magnetic field produced by either wire, which is represented as...

B_total=2*μ_i*I*cos(θ)/(2*π*√(.1²+(.011/2)²))

where cos(θ) = .1/√(.1²+(.011/2)²))

So B_total = 3.868e-5 T but it is telling me that is wrong.

Thanks for any help, it is greatly appreciated.

 

[Simon Bridge]

I think your reasoning runs the same as mine and I get a different answer - recheck your working and makes sure you plugged int he right values for things you have not given values for above. Check your arithmetic too. Best practise is to do all the algebra before you plug in values - so derive the relation you need using the variables given in the problem statement (d, R etc) first.

 

[TSny]

where cos(θ) = .1/√(.1²+(.011/2)²))

I don't think this expression is correct.
Make sure that you're using a carefully drawn diagram when setting up the expression for cos(θ).

 

[ShotgunMatador]

I don't think this expression is correct.
Make sure that you're using a carefully drawn diagram when setting up the expression for cos(θ).

So cosθ = adjacent/hypotenus
in this case adjacent is R=.1
hypotenuse is from half of the distance d (.011/2 = .0055) so using Pythagoreans theorem, I got Hyp = .10015 m. using that instead I get the same value, i think the cosine isn't the issue.

 

[Simon Bridge]

The wires centers and point P form an isosceles triangle.
If we define $\theta$ to be the half-angle at P,
Then $\cos\theta = R/\sqrt{R^2+(d/2)^2}$
... which is an example of where doing the algebra with the variables makes things easier BTW.
Putting: d=0.011m and R=0.1m, and isn't that what OP wrote?

 

[TSny]

in this case adjacent is R=.1

Double check this. Can you post a picture of the triangle you are working with?

 

[ShotgunMatador]

Double check this. Can you post a picture of the triangle you are working with?

here you go

 

[TSny]

The θ in this diagram is not the angle you want to use in cos(θ) for calculating the net B field. Did you draw the B fields for each wire?

 

[Simon Bridge]

Oh I see what happened there ... I was wondering:

So the y components at point P are equal but opposite...

... easy to miss.

 

[ShotgunMatador]

so the top wire would be counter clockwise and the bottom would be clockwise. the y component of B for the top wire points up and the y component of B for the bottom points down, don't they cancel?

 

[TSny]

so the top wire would be counter clockwise and the bottom would be clockwise. the y component of B for the top wire points up and the y component of B for the bottom points down, don't they cancel?

Yes, they cancel.

But you need to draw the arrows representing the B-field vectors at P for each wire so that you can see the angle they make to the horizontal.

 

[ShotgunMatador]

is the angle 45 because it will be tangent to the field line? aka there is a 90 degree angle between the two components

 

[TSny]

is the angle 45 because it will be tangent to the field line? aka there is a 90 degree angle between the two components

The B vectors are tangent to the circular field lines, but why would that produce a 45^o angle? You might try making several sketches for different positions of P. Do the B vectors make the same angle with respect to the horizontal for all positions of P?

 

[ShotgunMatador]

okay so it isn't 90, I the angle for the field will be the other angle in that triangle (see sketch), but when I tried it, it too gave me the wrong answer.

 

[ShotgunMatador]

The B vectors are tangent to the circular field lines, but why would that produce a 45^o angle? You might try making several sketches for different positions of P. Do the B vectors make the same angle with respect to the horizontal for all positions of P?

just kidding I plugged it in wrong.

Thanks for your help!