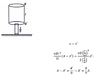
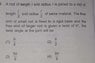Perhaps I can give an input here if may, even though I don't know how to work this problem completely yet. This problem is the rotational twisting version of what would be a linear elasticity type problem if the torque/twisting were replaced by a tension ## T ##. In the case of a vertical pulling force of ## F ## , a tension ## T =F ## would be created in the whole system, and the two parts would get stretched according to an equation of the form ## \frac{\Delta L_i}{L_i}=\alpha_i T ## where ## \alpha_i ## would depend upon some elasticity constant of the material, in the form of ## \alpha_i=\frac{b}{A_i }## where ## b ## is an elasticity property of the material, (the same for both if the material is the same) and ## A_i ## is the cross-sectional area. (Here I needed to google this to get what is common vocabulary: ## b ## here is the inverse of Young's modulus for the material). ## \\ ## Again, the twisting problem is the rotating version of the linear elasticity problem. I would need to google it to learn the details, but it is analogous to the linear elasticity problem. In the case of the linear problem, the item of interest would be the stretching of the bottom section that occurs. For this problem, the twisting that occurs on the lower section needs to be computed. ## \\ ## In this problem, they don't give ## \tau ## which would be the equivalent of ## T ## for the linear problem, but rather ## \Delta \theta_{total} ## which would be the equivalent of ## \Delta L_{total}=\Delta L_1+\Delta L_2 ## for the linear problem. ## \\ ## Editing: I think I see what their solution is, and the use of the letter ## A ## for angle is very clumsy: Basically the equation of interest is ## \Delta \theta_i=\tau (\frac{2 L_i}{\pi B_i r_i ^4}) ##. The rest is quite straightforward... How you do the algebra, to make it as simple as you can, is a matter of choice. You can solve for ## \tau ## first, but there are a couple of shortcuts that will allow you to find ## \Delta \theta_2 ##, without actually solving for ## \tau ##. In the solution presented, they set the ## \tau's ## equal. That's one possible approach, but the algebra can be done in a couple of ways.