To find the angle between the ground and rods in limiting friction

[gnits]

Homework Statement

To find the angle between the ground and rods when in limiting friction

Relevant Equations

force balancing and moments

Could I please ask for help with the following:

Here's my diagram:

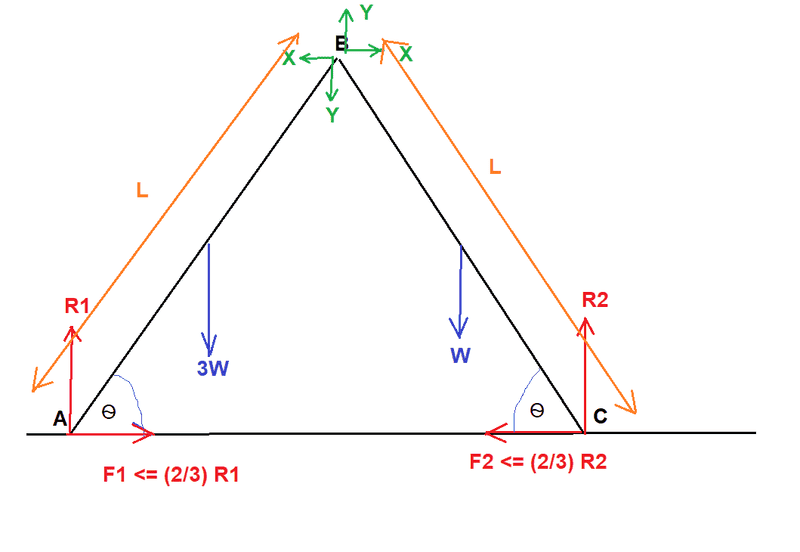
The forces at the hinge (green) are internal forces.

For the whole system resolving vertically gives:

R1 + R2 = 4W

and horizontally gives:

F1 = F2

For the rod of weight 3W only, taking moments about B gives:

F1 * L * sin(Ѳ) + 3W * (1/2) * L * cos(Ѳ) = R1 * L * cos(Ѳ)

When in the limiting situation I can replace F1 with (2/3) * R1 and rearrange to give:

(2/3) * tan(Ѳ) = 1 - ( 3W / (2 * R1) )

For the rod of weight W only, taking moments about B gives:

R2 * L * cos(Ѳ) = F2 * L * sin(Ѳ) + W * (L/2) * cos(Ѳ)

When in the limiting situation I can replace F2 with (2/3) * R2 and rearrange to give:

(2/3) * tan(Ѳ) = 1 - ( W / (2 * R2) )

Now, and maybe this is bad reasoning?, we always have that F1 = F2, so in the limiting situation when either F1 = (2/3) * R1 or F2 = (2/3) * R2 then we will have that R1 = R2.

So, from the above equations, replacing R2 with R1, I will have:

For rod of weight 3W:

(2/3) * tan(Ѳ) = 1 - ( 3W / (2 * R1) )

and for rod of weight W:

(2/3) * tan(Ѳ) = 1 - ( W / (2 * R1) )

And the latter is the larger value and so the latter has the larger value of Ѳ in the limiting case and so rod BC will be the one which slips.

This agrees with the book answer.

However, for the next part, determining the angle, I do not get the book answer of 45 degrees.

Here I equate my two equations to give:

1 - (3*W) / (2 * R1) = 1 - W / (2 * R2)

which gives:

R1 = 3 * R2

and using R1 = 4W - R2 leads to R2 = W

Which, if put back into the expression for (2/3) tan(Ѳ) above, leads to tan(Ѳ) = 3/4

which does not imply that Ѳ = 45 degrees.

Where did I go wrong?

Thanks for any help.

 

[BvU]

then we will have that R1 = R2.

This is only the case if both limiting situations apply at the same time.
But it is very likely they do not.

$\$

 

[gnits]

Thanks for your reply. I have solved it now by starting over with another, less complicated route.

 

[Lnewqban]

Thanks for your reply. I have solved it now by starting over with another, less complicated route.

Could you show us that less complicated route?

 

[gnits]

Sure. My simpler method was to consider the system as a whole and take moments about A and then about C, these lead straight to R2 = 3W/2 and R1 = 5W/2. Then, looking at the conditions for no slipping at A and then C leads to F1 <= 5W/3 and F2 <= W and so slipping will occur at C as frictional forces will reach W before 5W/2. Finally, considering the rod of weight W only, take moments about B and this leads to 2 * F2 * tan(Ѳ) = 2 * R2 - W and in the limiting case we know F2 and R2 in terms of W and so can solve for Ѳ and this gives Ѳ = 45 degrees. My original method, even when corrected for the problem that was pointed out, still had ambiguities related to mixing of limiting cases at A and C, this new method does not suffer from this.

 

[Lnewqban]

Sure. My simpler method was to consider the system as a whole and take moments about A and then about C, these lead straight to R2 = 3W/2 and R1 = 5W/2. .

. My original method, even when corrected for the problem that was pointed out, still had ambiguities related to mixing of limiting cases at A and C, this new method does not suffer from this.

Thank you very much, gnits.