SUMMARY
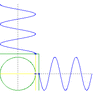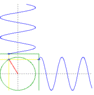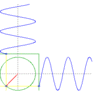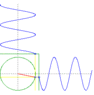
The discussion centers around the behavior of waves moving at right angles and out of phase, specifically examining how this results in circular motion. Participants reference the mathematical relationship x² + y² = A² to illustrate that sinusoidal functions can create circular paths. The conversation highlights the distinction between wave patterns and Lissajous figures, emphasizing that while two orthogonal sinusoidal waves can produce circular motion, they do not inherently create waves that move in circles without specific conditions, such as using a circular trough.
PREREQUISITES
- Understanding of sinusoidal functions and their properties
- Familiarity with wave mechanics and interference patterns
- Knowledge of Lissajous figures and their significance in wave analysis
- Basic principles of oscillation and wave equations
NEXT STEPS
- Research Lissajous figures and their applications in wave analysis
- Explore the mathematical derivation of wave interference patterns
- Study the principles of guided waves and their generation
- Examine the effects of phase differences in wave interactions
USEFUL FOR
Physics students, wave mechanics enthusiasts, and anyone interested in the mathematical modeling of wave behavior and interference patterns.