- #1
Vriska
- 138
- 2
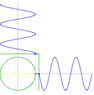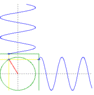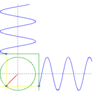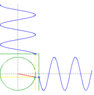
ylet x = Asinx, y = Acosx, apparently x^2 + y^2 = A^2 so this combination goes in circles. wot?
creating waves in a pool 90 degrees off and out of phase by 90 will make it move in circles? I'm skeptical, anyone have a video of an experiment that demonstrates this?
creating waves in a pool 90 degrees off and out of phase by 90 will make it move in circles? I'm skeptical, anyone have a video of an experiment that demonstrates this?