Shaddyab
- 19
- 0
1) Linear fit
I am running an experiment to find the linear relation between displacement (X) and voltage reading (V) of the measurement, when fitting a linear line to my measured data, such that:
V= m*X + b;
Based on the following links http://en.wikipedia.org/wiki/Regression_analysis (under Linear regression)
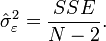
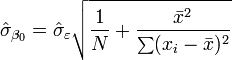
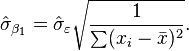
and
http://en.wikipedia.org/wiki/R-squared ( under Definitions)
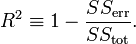
I can find the The standard errors of 'm' and 'b' parameters, Sm and Sb, respectively. and R-squared
So the Uncertainty of my measurement is :
m -/+ Sm
and
b -/+ Sb
But I would like to use the fit in the following way :
x=(V-b)/m
How can I relate the fit error to this form of the equation ?
2) Non-Linear fit
In the second experiment I have the following cubic fit:
X= a3 * (V ^3) + a2 * (V ^2) + a1 * (V) + a0
How can I find the uncertainty of a3, a2, a1, and a0 ? because I could not find any reference for doing so.
Can I use the same formula I used in the linear case to find the R-squared here for the non-linear fit?
I am running an experiment to find the linear relation between displacement (X) and voltage reading (V) of the measurement, when fitting a linear line to my measured data, such that:
V= m*X + b;
Based on the following links http://en.wikipedia.org/wiki/Regression_analysis (under Linear regression)
and
http://en.wikipedia.org/wiki/R-squared ( under Definitions)
I can find the The standard errors of 'm' and 'b' parameters, Sm and Sb, respectively. and R-squared
So the Uncertainty of my measurement is :
m -/+ Sm
and
b -/+ Sb
But I would like to use the fit in the following way :
x=(V-b)/m
How can I relate the fit error to this form of the equation ?
2) Non-Linear fit
In the second experiment I have the following cubic fit:
X= a3 * (V ^3) + a2 * (V ^2) + a1 * (V) + a0
How can I find the uncertainty of a3, a2, a1, and a0 ? because I could not find any reference for doing so.
Can I use the same formula I used in the linear case to find the R-squared here for the non-linear fit?