Understanding Feynman's Relativistic Electric Field Equation

[bryanso]

TL;DR

Want to understand why the radiation term in Feynman's relativistic electric field equation (Eq. 28.3) is inversely proportional to distance

Feynman's Lectures, vol. 1 Ch. 28, Eq. 28.3 is

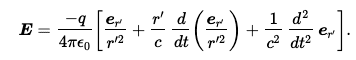
$r'$ is the distance to the apparent position of the charge. Feynman wrote,

"Of the terms appearing in (28.3), the first one evidently goes inversely as the square of the distance, and the second is only a correction for delay, so it is easy to show that both of them vary inversely as the square of the distance. All of the effects we are interested in come from the third term, which is not very complicated, after all. What this term says is: look at the charge and note the direction of the unit vector (we can project the end of it onto the surface of a unit sphere). As the charge moves around, the unit vector wiggles, and the acceleration of that unit vector is what we are looking for. That is all. Thus

is a statement of the laws of radiation, because that is the only important term when we get far enough away that the fields are varying inversely as the distance."

I don't understand why this acceleration is inversely proportional to $r'$?

Is that simply because the size of an object is inversely proportional to distance (perception) thus acceleration should be the same? Shouldn't $\frac{1}{r}$ appear somewhere?

(BTW this equation is extremely elegant but doesn't seem to be widely described in other texts.)

 

[Frodo]

I have long since forgotten so cannot give you a simple answer. But a hint of what to look for may help.

You need to be searching (internet, wiki etc) for far field as opposed to near field.

It is the far field which allows radio waves to propagate vast distances with enough signal strength to be picked up by receivers. The near field falls to negligible much quicker.

See Liénard–Wiechert potential and Electromagnetic radiation - Near and far fields and Near and far field and Near-Field vs. Far-Field.

Also, if you read further you get to Equation 28.5, which has the same third term you quote; and 28.6, derived from it, which has the 1/r term included. I haven't worked through the derivation to see how it arrives - I suspect it comes from the definition of er' and its derivative d^2/dt^2 er'.

See Chapter 21 - Solutions of Maxwell’s Equations with Currents and Charges in Volume 2 which repeats the equations as 21.1 and 21.1' - they are the same as in Volume 1 Chapter 28.

There are a number of web sites which list errors in the various editions of Feynman's (wonderful) Lectures.

Also, I don't think this should be in Special and General Relativity - it should be in Classical Physics where you will also find numerous similar posts - search on radiation.

 

[Frodo]

I don't understand why this acceleration is inversely proportional to $r'$?

Read further and you will see how the third term in Eqn 28.3 evaluates to Eqn 28.6 where you see the 1/r term.

(BTW this equation is extremely elegant but doesn't seem to be widely described in other texts.)

See the footnote in Vol 2, Chap 21

The formula was first published by Oliver Heaviside in 1902. It was independently discovered by R. P. Feynman, in about 1950, and given in some lectures as a good way of thinking about synchrotron radiation.

As an aside, I often find it useful not to worry too much if, on my first reading, I don't understand the full detail of something. I find it useful to continue as the following information often helps to elucidate the meaning. When I then go back it is usually easier to understand it.

Don't forget Rutherford's quotation:

All of physics is either impossible or trivial. It is impossible until you understand it, and then it becomes trivial.

 

[bryanso]

Thanks a lot. Great insights.