Understanding Function Notation in Higher Level Mathematics

[Artimodes]

Hello everyone,

I'm a newcomer to this forum! I've been having particular difficulty lately with understanding function notation in higher level mathematics. I felt like it was a general post so I posted in the general math section. I've finished calculus 3 and am going to take engineering math (basically ODE and applications) next spring.

It is my understanding that for a three dimensional function, for example an elliptic paraboloid, it's written like:

f(x,y)= z =x²+y²

However, after looking at Paul's Online Notes on ODE here, he starts to describe Newton's Second Law as a differential equation. I knew that, but his notation threw me off:

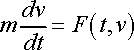
Is force in this case a three dimensional function, due to force being a function of the derivative of velocity while velocity is a function of time? Just confused.

Thanks for any help

 

[Bacle2]

I don't know if it is helpful to refer to the function as being 3-dimensional , or functions

being n-dimensional. Strictly speaking, the graph is 2-dimensional, but it lives

in 3-dimensional space. In the sense of F(t,v) , you can say that F depends on two

parameters, and, if you were to graph force using axes for t,v the (two-dimensional)

graph would live in 3-D.