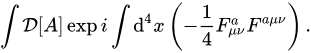Understanding Ghost Fields in QED: Eliminating Unphysical Degrees of Freedom"

[The Tortoise-Man]

I have a question about following statement about ghost fields in found here :
It states that introducing some ghost field provides one way to remove the two unphysical degrees of freedom of four component vector potential $A_{\mu}$ usually used to describe the photon field, since physically the light has only two allowed polarizations in the vacuum.

I not understand it completely how adding such a ghost field helps to remove the two unphysical degrees of freedom? Could somebody borrow some time to write the argument out?

I would also remark that it is known that in case of photon introducing a ghost field is so far I know NOT the only method to remove unphysical degrees of freedom: one could also do it in more old fashioned manner by imposing additionally a vanishing condition $\partial_{\mu} A_{\mu}=0$ on the field. But the concern of this question is really about how to use ghost field method to remove the unphysical degree.

 

[Demystifier]

In short, the contributions from ghosts cancel with the contributions from the unphysical degrees.

 

[The Tortoise-Man]

In short, the contributions from ghosts cancel with the contributions from the unphysical degrees.

Just to clarify: Do you refer to the "contributions" of the ghost field to the action functional (in sense of path integral formalism) formed with resp to the free Lagrangian for field $A_{\mu}$ when we add additionally the "ghost term", right? Is that what you mean the contributions coming from ghosts?

But then, which role plays in this context to take a gauge fixing condition like eg "$\partial^{\mu} A_{\mu}=0$"?

 

[Demystifier]

Do you refer to the "contributions" of the ghost field to the action functional

Not exactly, because I was talking about cancellation of contributions, and cancellation does not occur at the level of action. It occurs at the level of transition probability amplitudes (usually computed with Feynman diagrams).

 

[The Tortoise-Man]

Not exactly, because I was talking about cancellation of contributions, and cancellation does not occur at the level of action. It occurs at the level of transition probability amplitudes (usually computed with Feynman diagrams).

I see presumably. And in this whole procedure of adding this ghost term, should one also carry somewhere in the construction about implementing a gauge fixing term ( eg one proportionally to $\partial^{\mu} A_{\mu}=0$), or is this issue with "adding a gauge fixing term" remedied automatically after having added the ghost term, so one shouldn't care there about any more?

 

[Demystifier]

I see presumably. And in this whole procedure of adding this ghost term, should one also carry somewhere in the construction about implementing a gauge fixing term ( eg one proportionally to $\partial^{\mu} A_{\mu}=0$), or is this issue with "adding a gauge fixing term" remedied automatically after having added the ghost term, so one shouldn't care there about any more?

It's remedied automatically, because the ghost term depends on the gauge fixing term.

 

[vanhees71]

Another example, where the idea of the Faddeev-Popov ghostfield becomes clear, applying it to QED and the black-body radiation. If you write down the naive path-integral expression of the logarithm of the partition sum, $\Omega=\ln Z$, for free photons in Feynman gauge you get the partition function for four massless bosonic degrees of freedom. The FP ghosts are formally two massless scalar fields but quantized as fermions, which give two bosonic degrees of freedom but contributing with the opposite sign to $\Omega$. So you are left with two bosonic degrees of freedom, as it should be, since any massless boson with spin $s \neq 0$ has 2 polarization degrees of freedom (two helicity eigenstates).

 

[Demystifier]

@vanhees71 can you give a reference where such computation of $\Omega$ is performed?

 

[vanhees71]

Within the path-integral formalism, see Sect. 3.5 in

https://itp.uni-frankfurt.de/~hees/publ/off-eq-qft.pdf

The path-integral formalism is, of course, a bit overcomplicating the issue, because of the delicate issue to regulate the functional determinant. I've used the heat-kernel method. Alternatively you can use some operator formalism. For QED the most simple is to work with the gauge fixed radiation-gauge formalism. Another way is the manifestly Poincare covariant Gupta-Bleuler formalism or BRST quantization (which then can also be extended to the non-Abelian case).

 

[The Tortoise-Man]

It's remedied automatically, because the ghost term depends on the gauge fixing term.

Thank you, I think the rough idea is clearer now, let me try to rephrase how I understood it up to now (...for sake of simplicity only for QED / photon field since I'm concerned only about rough idea):

We have integral$\int \mathcal{D}[A] \exp (i \int \mathrm d^4 x \left ( - \frac{1}{4} F^a_{\mu \nu} F^{a \mu \nu } \right ))= \int \mathcal{D}[A] \exp (i S[A])$

running over all(!) configurations (physical equiv ones and not; so we have at that point all these redundances), where

$S[A] =\int \mathrm d^4 x \left ( - \frac{1}{4} F^a_{\mu \nu} F^{a \mu \nu } \right )$ the action for a fixed configuration.

The first double integral above is up to approp constant essentially the transition probability amplitude and these FD-fields intuitively if I understand the story correctly help to split up this integral into product two integrals, where one is running over phyically inequiv configurations (the physical part) and one over gauge group (the redundance part; which we intuitively want to uncouple), right?How should we do it practically most "usually" (=lecture book strategy)?

My guess/ what I found so far: We pick (so explit choices cannot be avoided) a functional $G[A]$ on field configs $A$ such that it imposes gauge fixing condition $G[A]=0$, eg $G[A]= \partial^{mu} A_{\mu} =0$, but there is myriad of others, just a choice!

What's next. What I found in the net is following strategy:

A lengthy calculation shows (lets take it as black box) that

$1 = \int \mathcal{D}[\alpha (x) ] \delta (G(A^{\alpha })) \mathrm{det} \frac{\delta G(A^{\alpha} )}{\delta \alpha }$

where the integral runs over gauge trafos $\alpha$ performing $A \mapsto A_{\alpha}:= A_{\mu}(x)+ c \cdot \partial_{\mu} \alpha(x)$ and then insert this identity into the first integral above.Seemingly reordering the terms in the integral carefully gives the desired splitting in integrals running over physical / unphysical configurations.

The ghost fields should somehow arise from determinant term, which $\mathrm{det} \frac{\delta G(A^{\alpha} )}{\delta \alpha }$, which in turn by definition depends explicitly on the choice of the functional determining the gauge fixing condition.

By the way: Is that exactly what you meant in #6 in "because the ghost term depends on the gauge fixing term."?

So say we have extracted from the determinant two fields (...or let me say better we found in determinant expression two terms, which we interpret as these two ghost fields) , which become later our FD-ghosts.

But then, if what I wrote so far is a correct rephrasing of the idea behind implementing FD-ghosts, how this strategy leads finally to the desired splitting of the integral above in the described two factors, the integrals running over "physical" and "unphysical" parts?

Could you sketch the idea how finally to obtain this splitting?