Understanding Lyapunov Exponent: Why Do We Use an Exponential Function?

[ATY]

Hey guys,
I need your help. I am not sure if this is the right part of the forum to ask this question.

So I started reading papers about the Lyapunov Exponent, but there is something I do not understand in the formula. Why

? It seems logical that we want

because we want to get the Exponent at a certain point and therefore the startingpoints should be really close together.
I added a text from a book which says, that we have

, because then my

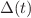will fluctuate around a finite value, but I have no clue why an exponential function should do this. Maybe somebody can help me.

 

[Filip Larsen]

I am a bit rusty on this topic, but let me give it a try.

I am guessing that the fluctuations of Δ(t) around a finite value that the text mentions is a reference to what happens when forming the inner limit, so to speak. The initial exponential expansion phase is when the two originally very close orbits follow each other around in the same branch of the Lorenz attractor and the fluctuation then occur when when the orbits around some value of t separate into each branch and the state of the two orbits becomes uncorrelated. Another way to say it is that the fluctuations only occur if you take the outer limit before the inner limit (as the text also warns about will give a different result). If you take the inner limit first, it can be replaced by a measure that is similar to how you define the differential coefficients and once that limit is made there is no fluctuation.

The outer limit is then needed to make a kind of integral along the orbit. For instance, for an orbit to be chaotic the flow around the orbit must in net be exponentially expanding over all times and not just during any initial transient.