evinda said:
Oh yes, I forgot to write it. I am sorry...
Could you maybe explain me how, given a graph of a set, we deduce if the given set is open or closed?
I haven't really understood how this can be done.. (Sweating)
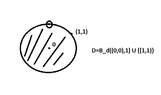
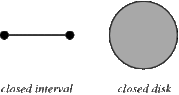
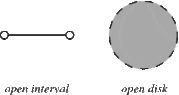
Naively, we look at the "edges". For a 1-manifold (a curve), this is the endpoints. For a 2-manifold (a surface) this is the perimeter. For a 3-manifold, this is the surface. In general, the boundary of an $n$-manifold is a $n-1$-manifold.
That said, this is the intuition of a very "special" kind of space (Euclidean space, with the Euclidean metric), and certain "simple" sets, built out of smooth maps of (respectively): intervals, disks, and spheres. In an arbitrary topological space, we only have the definitions to fall back on, as our intuition may fail us. Some very "bizarre" neighborhood systems can be constructed, with unexpected properties.
Not only that, but the power set of even the real line is...quite large. So there are a LOT of possible sets to examine. One cannot hope to be able to examine, or even classify, them all. Arbitrary functions of a real interval can be quite bizarre, and even limiting our attention to continuous functions isn't much better.
Open sets (in the real line these are unions of open intervals, in the real plane, these are unions of open disks...in the USUAL (metric) topology) is one way to "filter" this bewildering array of sets, to be able to speak about "homeomorphs" of regions (areas that are topologically equivalent, even though they may "look" radically different).
In analysis, metrics serve as a gauge of "good approximation". If a function stays within certain bounds, for example, we mean its graph (on the domain of definition) lies within a closed set. Ideally, we can show a sequence of functions lie within a sequence of ever-decreasing closed sets. Note "within" here means in the INTERIOR of said closed sets, and we can form a FILTER from the sequence of these interiors. If this filter is finer (i.e. contains more sets than) the neighborhood filter for our function space, we have a notion of CONVERGENCE. This allows us to take LIMITS of functions, not just limits of the individual points of definition, or individual image points. This is a VERY powerful tool.
Bound up with all of this, is the concept of "nearness" (spatial "closeness"). Here is a proper definition:
A point $P$ is
near a set $A$ (written $A \leftarrow P$) if for every neighborhood $N(P)$, we have:
$N(P) \cap A \neq \emptyset$.
Some obvious consequences of this definition:
1. If $P \in A$, then $A \leftarrow P$.
2. If $P \in \partial A$, then $A \leftarrow P$.
3. If $P$ is in the interior of $X\setminus A$, then $P$ is not near $A$.
If every point of $A$ is not near $X\setminus A$, then $A$ is open. Near points can be thought of as the points in or "touching" (the corresponding geometric term is "tangent") a set $A$.
The re-casting of the term "continuous" in nearness-terms is particularly satisfying:
$f$ is continuous if $A \leftarrow P \implies f(A) \leftarrow f(P)$
capturing our usual intuition that continuous functions don't cause "tears" in the sets they transform.
Huh. It's a lot to process, eh?
It's really hard, as I said earlier, to just "look at the picture". To really "prove" a set is open, one often HAS to use the definitions. Here is an example:
Let's PROVE that the set $A = (0,1]$ is not open. We will consider two cases:
1. $x \in (0,1)$
2. $x = 1$
In case 1, we will show $\Bbb R\setminus A \leftarrow x$ is false.
We have: $0 < x < 1$, so let $\epsilon = \frac{1}{2}\min(x,1-x)$
Since $0<x$ and $x< 1$, so that $0 = 1-1 < 1-x$, we have $\epsilon > 0$ (half of a positive number is still positive).
Let $N(x) = (x-\epsilon,x+\epsilon) = B_d(x,\epsilon)$.
Then $N(x) \subseteq (0,1)$ but $N(x) \cap \Bbb R\setminus A = \emptyset$, so $x$ is not near $\Bbb R\setminus A$ (recall that if $x$ is near a set, EVERY neighborhood has to intersect it, and we found a counter-example).
So in case, 1, we have actually proven $(0,1)$ is open. But, we're not done yet.
Now suppose $x = 1$. Let $N(1)$ be ANY neighborhood of $1$. Then, since $N(1)$ is a neighborhood, there is some $B_d(1,\epsilon)$ for some $\epsilon > 0$, with $B_d(1,\epsilon) = (1-\epsilon,1+\epsilon) \subseteq N(1)$. Without loss of generality, if $\epsilon \geq 1$, we can replace it with $\frac{1}{\epsilon + 1}$ (this will still be inside $N(1)$), so we will assume that $\epsilon < 1$.
Now $1 - \epsilon < 1$, and $0 = 1 - 1 < 1 -\epsilon$, so for any $y \in (1-\epsilon,1) \subset B_d(1,\epsilon) \subseteq N(1)$ we have $y \in N(1)$ and $y \in A$, thus $N(1) \cap A \neq \emptyset$.
This shows $1$ is near $A$.
On the other hand, $1 + \epsilon > 1$, so for any $y \in (1,1+\epsilon) \subset B_d(1,\epsilon) \subseteq N(1)$, we also have $y \in \Bbb R\setminus A$, so $N(1) \cap \Bbb R\setminus A \neq \emptyset$.
This shows that $1$ is near the complement of $A$ in $\Bbb R$, that is, it is a boundary point of $A$ (near $A$ and its complement), and open sets do not contain any boundary points. Hence, $A$ is not open.
Now, this is a lot "harder" than just looking at a picture, but this is what is actually involved in "nailing it down air-tight".