chwala
Gold Member
- 2,828
- 423
- Homework Statement
- see attached
- Relevant Equations
- Ring Theory
My interest is on the highlighted part ...

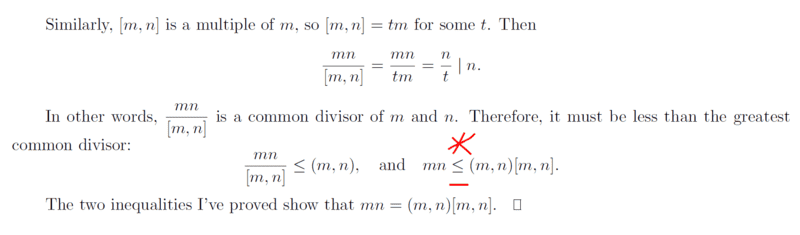
Now to my question,
in what cases do we have ##mn<(m,n)[m,n]?##
I was able to use my example say,
Let ##m=24## and ##n=30## for example, then
##[m,n]=120## and ##(m,n)=6## in this case we can verify that,
##720=6⋅120## implying that, ##mn≤ (m,n)[m,n]##.
Now to my question,
in what cases do we have ##mn<(m,n)[m,n]?##
I was able to use my example say,
Let ##m=24## and ##n=30## for example, then
##[m,n]=120## and ##(m,n)=6## in this case we can verify that,
##720=6⋅120## implying that, ##mn≤ (m,n)[m,n]##.