DBTStud
- 4
- 0
- TL;DR
- I need to derive an equation for the mechanical advantage between the piston force and the force at the wall. I need help to get the right answer
Hi all,
I need to derive an equation for the mechanical advantage between the force applied at the wall and the force at the piston for a linked system. I have attempted this but my equation suggests that the wall force increases expenantionally as the connecting rod approaches the horrizontal.
I've attached my derrivation. He fixed pivot of the bellcrank is ridgedly attached to the vertical piston cylinder. The module works to push the complete unit from the wall.
Please can you suggest any modifications where I might have went wrong
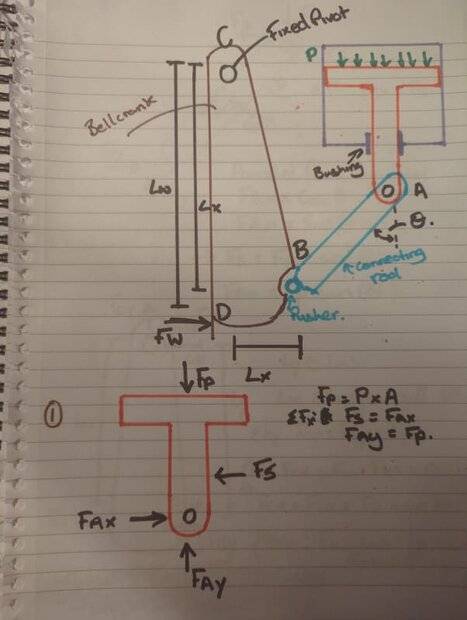
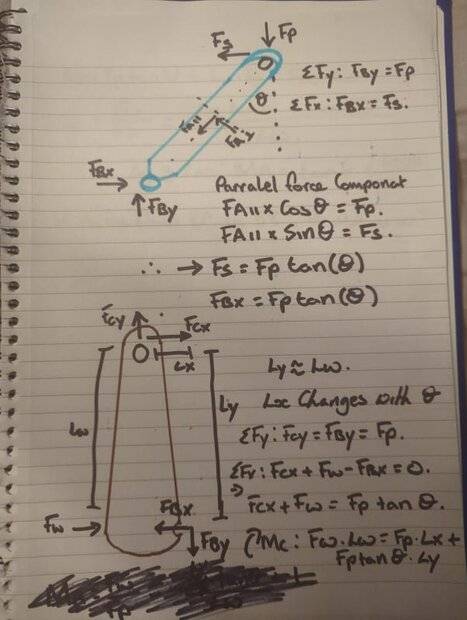
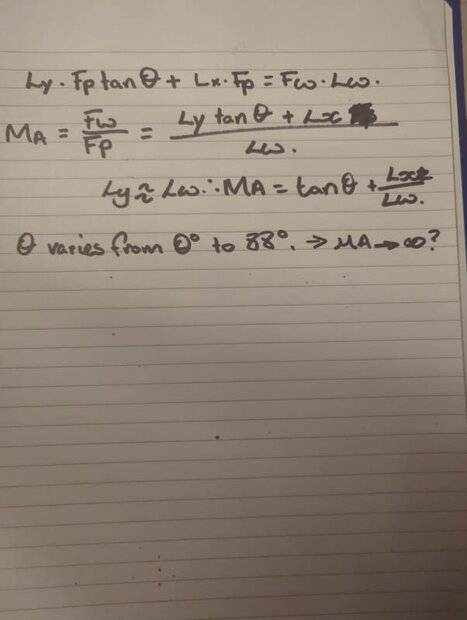
I need to derive an equation for the mechanical advantage between the force applied at the wall and the force at the piston for a linked system. I have attempted this but my equation suggests that the wall force increases expenantionally as the connecting rod approaches the horrizontal.
I've attached my derrivation. He fixed pivot of the bellcrank is ridgedly attached to the vertical piston cylinder. The module works to push the complete unit from the wall.
Please can you suggest any modifications where I might have went wrong