Understanding the Quadratic Formula: Why the Negative Root is Not Considered

[davon806]

Homework Statement

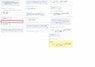
Please see the method of solving the equation x^3 -4x^2 + 4x +2 = 0 from the attached.
In the red brackets,can anyone explain why the negative root is not involved in the calculation?
by the quadratic formula,
z = [y±√(y^2 - 4k)]/2
so why only y+√(y^2 - 4k) is considered?
and in the second bracket,again,why the another root of u ,(-1/27)(-35 - 3√129),is not used?
Both roots are negative.
Thx.

Homework Equations

The Attempt at a Solution

 

[tiny-tim]

hi davon806!

In the red brackets,can anyone explain why the negative root is not involved in the calculation?
…
and in the second bracket,again,why the another root of u ,(-1/27)(-35 - 3√129),is not used?

you can use the "negative" root in either or both cases, and it should give the same result in the end …

have you tried it? ​

 

[davon806]

As there are 2 solutions of z and 2 solutions of u,
there are 4 possible answers for x
z = [y ± √(y^2 - 4k)]/2 , u = 1/27(-35 ± 3√129)
if both of the signs are +,or both signs are -,the value of x would be:
x = 4/3 - 4/[3(35-3√129)^(1/3) - 1/3(35-3√129)^(1/3)]
if z = [y+√(y^2 - 4k)]/2 and u = (-35-3√129)/27 ,
x = 4/3 - 4/[3(35+3√129)^(1/3) - 1/3(35+3√129)^(1/3)]

What's wrong?Thx.

 

[tiny-tim]

hi davon806!

x = 4/3 - 4/[3(35-3√129)^(1/3) - 1/3(35-3√129)^(1/3)]
if z = [y+√(y^2 - 4k)]/2 and u = (-35-3√129)/27 ,
x = 4/3 - 4/[3(35+3√129)^(1/3) - 1/3(35+3√129)^(1/3)]

ah, but 1/(35-3√129) = (35+3√129)/64